
МЕЖГОСУДАРСТВЕННЫЙ СОВЕТ ПО СТАНДАРТИЗАЦИИ,
МЕТРОЛОГИИ И СЕРТИФИКАЦИИ
(МГС)
INTERSTATE COUNCIL FOR
STANDARDIZATION, METROLOGY AND CERTIFICATION
(ISC)
|
РЕКОМЕНДАЦИИ |
РМГ |
Государственная система обеспечения
единства измерений
ПОКАЗАТЕЛИ
ТОЧНОСТИ,
ПРАВИЛЬНОСТИ, ПРЕЦИЗИОННОСТИ МЕТОДИК
КОЛИЧЕСТВЕННОГО ХИМИЧЕСКОГО АНАЛИЗА
Методы оценки
Москва
ИПК Издательство стандартов
Предисловие
Цели, основные принципы и основной порядок проведения работ по межгосударственной стандартизации установлены ГОСТ 1.0-92 «Межгосударственная система стандартизации. Основные положения» и ГОСТ 1.2-97 «Межгосударственная система стандартизации. Стандарты межгосударственные, правила и рекомендации по межгосударственной стандартизации. Порядок разработки, принятия, применения, обновления и отмены»
Сведения о рекомендациях
1 РАЗРАБОТАНЫ Федеральным государственным унитарным предприятием «Уральский научно-исследовательский институт метрологии» (ФГУП «УНИИМ»)
2 ВНЕСЕНЫ Госстандартом России
3 ПРИНЯТЫ Межгосударственным советом по стандартизации, метрологии и сертификации (протокол № 23 от 22 мая 2003 г.)
За принятие проголосовали:
|
Краткое
наименование страны |
Код страны |
Сокращенное наименование национального органа по стандартизации |
|
Азербайджан |
AZ |
Азстандарт |
|
Армения |
AM |
Армстандарт |
|
Грузия |
GE |
Грузстандарт |
|
Казахстан |
KZ |
Госстандарт Республики Казахстан |
|
Кыргызстан |
KG |
Кыргызстандарт |
|
Молдова |
MD |
Молдова-Стандарт |
|
Российская Федерация |
RU |
Госстандарт России |
|
Таджикистан |
TJ |
Таджикстандарт |
|
Туркменистан |
TM |
Главгосслужба «Туркменстандартлары» |
|
Узбекистан |
UZ |
Узстандарт |
|
Украина |
UA |
Госпотребстандарт Украины |
4 Приказом Федерального агентства по техническому регулированию и метрологии от 27 октября 2004 г. № 48-ст рекомендации по межгосударственной стандартизации РМГ 61-2003 введены в действие в качестве рекомендаций по метрологии Российской Федерации с 1 января 2005 г.
5 ВВЕДЕНЫ ВПЕРВЫЕ
СОДЕРЖАНИЕ
РМГ 61-2003
РЕКОМЕНДАЦИИ ПО МЕЖГОСУДАРСТВЕННОЙ СТАНДАРТИЗАЦИИ
Государственная система обеспечения единства измерений
ПОКАЗАТЕЛИ ТОЧНОСТИ, ПРАВИЛЬНОСТИ, ПРЕЦИЗИОННОСТИ
МЕТОДИК КОЛИЧЕСТВЕННОГО ХИМИЧЕСКОГО АНАЛИЗА
Методы оценки
State system for ensuring the uniformity of measurements. Accuracy, trueness and precision measures
of the procedures for quantitative chemical analysis. Methods of determination
Дата введения - 2005-01-01
1 Область применения
Настоящие рекомендации распространяются на методики количественного химического анализа (далее - методики анализа), предназначенные для применения в ряде лабораторий, разрабатываемые и пересматриваемые в соответствии с ГОСТ 8.010, и определяют:
- точность, правильность, прецизионность (повторяемость и воспроизводимость) анализа - качественные характеристики анализа;
- показатели точности, правильности, прецизионности (повторяемости и воспроизводимости) методик анализа - количественные характеристики методик анализа;
- методы оценки показателей точности, правильности, прецизионности методик анализа.
Определенные в соответствии с настоящими рекомендациями показатели точности, правильности, прецизионности методик анализа используют при:
- оформлении свидетельств об аттестации методик анализа;
- оформлении соответствующих разделов документов, содержащих методики анализа;
- оформлении протоколов испытаний (контроля) продукции, анализа объектов;
- контроле качества результатов анализа.
Рекомендации не распространяются на методики количественного химического анализа неоднородных и не подлежащих гомогенизации проб объектов.
Настоящие рекомендации разработаны с учетом требований [1] - [5].
Условные обозначения и сокращения, используемые в рекомендациях, приведены в приложении А.
2 Нормативные ссылки
В настоящих рекомендациях использованы ссылки на следующие межгосударственные нормативные документы:
ГОСТ 8.010-901) Государственная система обеспечения единства измерений. Методики выполнения измерений
1) На территории Российской Федерации действует ГОСТ Р 8.563-96.
ГОСТ 8.315-97 Государственная система обеспечения единства измерений. Стандартные образцы состава и свойств веществ и материалов. Основные положения
ГОСТ 12.1.016-79 Система стандартов безопасности труда. Воздух рабочей зоны. Требования к методикам измерения концентрации вредных веществ
СТ СЭВ 543-77 Числа. Правила записи и округления
РМГ 29-99 Государственная система обеспечения единства измерений. Метрология. Основные термины и определения
РМГ 43-2001 Государственная система обеспечения единства измерений. Применение «Руководства по выражению неопределенности измерений»
РМГ 60-2003 Государственная система обеспечения единства измерений. Смеси аттестованные. Общие требования к разработке
МИ 1317-86 Государственная система обеспечения единства измерений. Результаты и характеристики погрешности измерений. Формы представления. Способы использования при испытаниях образцов продукции и контроле их параметров
Примечание - При пользовании настоящими рекомендациями целесообразно проверить действие ссылочных документов по указателю «Национальные стандарты», составленному по состоянию на 1 января текущего года, и по соответствующим информационным указателям, опубликованным в текущем году. Если ссылочный документ заменен (изменен), то при пользовании настоящими рекомендациями следует руководствоваться замененным (измененным) документом. Если ссылочный документ отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.
3 Термины и определения
В настоящих рекомендациях применяют следующие термины с соответствующими определениями с учетом [1] - [7], РМГ 43, РМГ 29, МИ 1317:
1 Методика анализа является разновидностью методики выполнения измерений.
2 В качестве измеряемой характеристики принимают содержание одного или ряда компонентов состава пробы.
3.3 результат анализа1): Среднее значение (среднее арифметическое или медиана) результатов единичного анализа.
3.4 результат единичного анализа (определения)2): Значение содержания компонента в пробе вещества (материала), полученное при однократной реализации процедуры анализа.
1) Результат анализа по сути представляет собой среднее п результатов измерений у (по [1]), полученных в условиях повторяемости при фиксированных значениях п.
2) «Результат единичного анализа» - аналог «результата измерений» по [1].
Примечание к 3.3 и 3.4 - В документе на методику анализа устанавливают: сколько (один или несколько) результатов единичного анализа (параллельных определений) должно быть выполнено, способы их усреднения и представления в качестве результата анализа. В самом простом случае (если методикой анализа не предусмотрено проведение параллельных определений) результат единичного анализа является собственно результатом анализа.
3.5 точность: Степень близости результата анализа к истинному (или в его отсутствие принятому опорному) значению ([1]).
3.6 правильность: Степень близости среднего значения, полученного на основе большой серии результатов единичного анализа, к истинному [или в его отсутствие принятому опорному (по 3.22, перечисления а), б), в)] значению (с учетом [1]).
3.7 прецизионность: Степень близости друг к другу результатов единичного анализа (результатов анализа), полученных в конкретных регламентированных условиях ([1]).
3.8 повторяемость: Прецизионность в условиях повторяемости ([1]).
3.9 условия повторяемости: Условия, при которых результаты единичного анализа получают по одной и той же методике на идентичных пробах в одинаковых условиях и практически одновременно (результаты параллельных определений) ([1]).
3.10 воспроизводимость: Прецизионность в условиях воспроизводимости ([1]).
3.11 условия воспроизводимости: Условия, при которых результаты анализа получают по одной и той же методике на идентичных пробах, но в различных условиях (разное время, разные аналитики, разные партии реактивов одного типа, разные наборы мерной посуды, экземпляры средств измерений одного типа, разные лаборатории) ([1]).
3.12 внутрилабораторная прецизионность: Прецизионность в условиях, при которых результаты анализа получают по одной и той же методике на идентичных пробах при вариации различных факторов (время, аналитики, реактивы и т.п.), формирующих разброс результатов при применении методики в конкретной лаборатории (с учетом ([1]).
3.13 показатели качества методики анализа (показатели точности, правильности, повторяемости, воспроизводимости): Приписанные характеристики погрешности методики анализа и ее (погрешности) составляющих.
3.14 приписанные характеристики погрешности методики анализа и ее (погрешности) составляющих: Установленные характеристики погрешности и ее составляющих для любого из совокупности результатов анализа (результатов единичного анализа)1), полученного при соблюдении требований и правил аттестованной методики анализа.
1) Используется для количественной характеристики повторяемости.
Примечания
1 Приписанные характеристики погрешности характеризуют гарантируемую точность методики анализа.
2 Эквивалентом приписанной характеристики погрешности является неопределенность. Согласно [6] неопределенность - это параметр, связанный с результатом измерения (в данном случае - анализа) и характеризующий разброс значений, которые с достаточным основанием могут быть приписаны измеряемой величине. Способы выражения и методы оценки неопределенности даны в [6], [7] и РМГ 43. При этом эквивалентом расширенной неопределенности является интервальная оценка приписанной характеристики погрешности, стандартной неопределенности - точечная оценка приписанной характеристики погрешности (см. табл. 1).
3.15 среднее квадратическое (стандартное) отклонение повторяемости: Среднее квадратическое отклонение результатов единичного анализа, полученных по методике в условиях повторяемости (с учетом [1]).
3.16 предел повторяемости: Допускаемое для принятой вероятности 95 % абсолютное расхождение между наибольшим и наименьшим из п результатов единичного анализа, полученных в условиях повторяемости (с учетом [1])2).
2) В [1] термин «предел повторяемости» приведен для п = 2. Поскольку в методиках анализа, как правило, предусмотрено получение результата анализа как среднего из п параллельных определений, при этом п ³ 2, этот термин приведен для п, регламентированного методикой анализа.
3.17 среднее квадратическое (стандартное) отклонение воспроизводимости: Среднее квадратическое отклонение результатов анализа, полученных в условиях воспроизводимости (с учетом [1]).
3.18 предел воспроизводимости: Допускаемое для принятой вероятности 95 % абсолютное расхождение между двумя результатами анализа, полученными в условиях воспроизводимости (с учетом [1])3).
3) В [1] этот термин приведен для двух результатов измерений. Термин «результат измерений» по [1] соответствует термину «результат единичного анализа».
3.19 систематическая погрешность методики анализа: Разность между математическим ожиданием результатов единичного анализа, полученных во всех лабораториях, применяющих данную аттестованную методику, и истинным [или в его отсутствие принятым опорным (по 3.22, перечисления а), б), в)] значением измеряемой характеристики (с учетом [1]).
3.20 систематическая погрешность лаборатории (при реализации методики анализа): Разность между математическим ожиданием результатов единичного анализа, полученных в отдельной лаборатории, и истинным [или в его отсутствие принятым опорным (по 3.22, перечисления а), б), в)] значением измеряемой характеристики (с учетом [1]).
Примечание - Модель погрешности, приведенная в настоящих рекомендациях, предусматривает получение результатов единичного анализа в отдельной лаборатории в условиях повторяемости.
3.21 лабораторная составляющая систематической погрешности: Разность между математическим ожиданием результатов единичного анализа, полученных в отдельной лаборатории при реализации методики анализа, и математическим ожиданием результатов единичного анализа, полученных во всех лабораториях, применяющих данную методику анализа (с учетом [1]).
3.22 принятое опорное значение: Значение, которое служит в качестве согласованного для сравнения.
Примечание - В методах оценки показателей качества методик анализа, рассмотренных в настоящих рекомендациях, в качестве опорного значения могут быть приняты:
а) теоретическое или научно установленное значение;
б) аттестованное значение стандартного образца;
в) аттестованное значение аттестованной смеси;
г) математическое ожидание измеряемой характеристики, т.е. среднее значение заданной совокупности результатов анализа - лишь в том случае, когда а), б) и в) недоступны.
3.23 нормы характеристик погрешности анализа; нормы погрешности: Значения характеристики погрешности результатов анализа, задаваемые в качестве требуемых или допускаемых.
Примечание - Нормы погрешности характеризуют требуемую точность анализа.
3.24 погрешность результата анализа (результата единичного анализа): Отклонение результата анализа (результата единичного анализа), полученного по аттестованной методике, от истинного (или в его отсутствие принятого опорного) значения.
Примечание - При опорном значении по 3.22, перечисление г) за погрешность принимают отклонение результата анализа (результата единичного анализа), полученного по аттестованной методике, от математического ожидания заданной совокупности результатов, полученных по этой методике.
4 Общие положения
4.1 Разработка методик анализа предусматривает установление приписанных характеристик погрешности.
4.2 Формы представления приписанных характеристик погрешности и ее составляющих (показателей качества методики анализа), а также их связь с качественными характеристиками анализа приведены в таблице 1.
Таблица 1 - Номенклатура и формы представления показателей качества методики анализа
|
Показатель качества (количественная характеристика) методики анализа |
Формы представления показателей качества методики анализа (приписанных характеристик погрешности и ее составляющих) |
|
|
Точность |
Показатель точности методики анализа - приписанная характеристика погрешности методики анализа |
Границы (Dн, Dв), в которых погрешность любого из совокупности результатов анализа находится с принятой вероятностью Р - интервальная оценка, или ±D, Р, при D = |Dн| = Dв = Zs(D), где Z - квантиль распределения, зависящий от его типа и принятой вероятности Р. Среднее квадратическое отклонение - s(D) погрешности результатов анализа, полученных во всех лабораториях, применяющих данную методику анализа, - точечная оценка |
|
Правильность |
Показатель правильности методики анализа - приписанная характеристика систематической погрешности методики анализа |
Θ, sс, где Θ - математическое ожидание (оценка) систематической погрешности методики анализа; s (Dс) - среднее квадратическое отклонение неисключенной систематической погрешности методики анализа - точечная оценка. Примечание - Θ может быть введена в результат единичного анализа в качестве поправки. |
|
Правильность |
Показатель правильности методики анализа - приписанная характеристика систематической погрешности методики анализа |
Границы (Dс.н, Dc.в), в которых систематическая погрешность методики анализа находится с принятой вероятностью Р - интервальная оценка, или ±Dc, Р, где Dс.в = |Dс.н| = Dс = Zsс |
|
Повторяемость |
Показатель повторяемости методики анализа - приписанная характеристика случайной погрешности результатов единичного анализа, полученных в условиях повторяемости |
Среднее квадратическое отклонение результатов единичного анализа, полученных по методике в условиях повторяемости - sr. Предел повторяемости1) - rп для п результатов параллельных определений, регламентируемых методикой анализа |
|
Воспроизводимость |
Показатель воспроизводимости методики анализа - приписанная характеристика случайной погрешности результатов анализа, полученных в условиях воспроизводимости |
Среднее квадратическое отклонение всех результатов анализа, полученных по методике в условиях воспроизводимости - sR Предел воспроизводимости2) - R для двух результатов анализа |
|
1) В национальных стандартах принято обозначение d. 2) В национальных стандартах принято обозначение D. |
||
4.3 Значения приписанных характеристик погрешности устанавливают для всего диапазона действия методики анализа.
4.4 Способы выражения приписанных характеристик погрешности должны соответствовать принятым в исходных данных на разработку (пересмотр) конкретной методики анализа.
4.5 Значения приписанных характеристик погрешности, рассчитанные в соответствии с настоящими рекомендациями, не должны превышать норм погрешности (при их наличии).
Примечание - Нормы погрешности - по 2.3.2 ГОСТ 8.010.
4.6 Приписанные характеристики погрешности указывают в единицах измеряемой величины (абсолютные) или в процентах (относительные) относительно результатов анализа. Допускается представлять приписанные характеристики погрешности в виде формул, таблиц, графиков.
4.7 Приписанные характеристики погрешности выражают числом, содержащим не более двух значащих цифр. Число получают округлением в большую сторону, если цифра последующего (неуказываемого младшего) разряда равна или больше пяти, или в меньшую сторону, если эта цифра меньше пяти - по СТ СЭВ 543.
- случайные различия между составами отобранных проб;
- матричные эффекты и взаимные влияния;
- неполнота извлечения, концентрирования;
- возможные изменения состава пробы вследствие ее хранения;
- погрешности используемых средств измерений, в том числе стандартных образцов (СО) или аттестованных смесей (АС), оборудования, а также чистота используемых реактивов;
- неадекватность математической модели, положенной в основу метода измерения;
- неадекватность образцов для градуировки анализируемым пробам;
- неопределенность значения поправки на холостую пробу;
- действия оператора;
- вариации параметров окружающей среды при проведении измерений (температура, влажность, загрязнение воздуха и т.д.);
- случайные эффекты.
4.9 Оценку значений приписанной характеристики погрешности - показателя точности методики анализа - проводят по установленным значениям характеристик ее случайной и систематической составляющих во всем диапазоне измерений содержания определяемого компонента, для всех диапазонов изменения сопутствующих компонентов (далее - влияющие факторы пробы), а также условий выполнения измерений, указываемых в документе на методику анализа.
4.10 Оценка показателей прецизионности (повторяемости и воспроизводимости) может быть проведена на однородных и стабильных рабочих пробах контролируемого вещества (материала) либо с применением СО по ГОСТ 8.315, либо АС по РМГ 60.
Примечание - Рабочие пробы должны быть однородны и стабильны по составу на все время проведения эксперимента.
4.11 Оценка показателя правильности методики анализа может быть проведена одним из следующих способов - с применением:
- набора образцов для оценивания в виде СО или АС;
- однофакторных планов эксперимента;
- аттестованной методики анализа с известными (оцененными) характеристиками погрешности (методики сравнения);
- метода добавок;
- метода добавок в сочетании с методом разбавления;
- расчетного способа (путем суммирования числовых значений составляющих систематической погрешности).
4.12 Краткие сведения об оценке показателей качества методики анализа излагают в приложении (справочном) к документу на методику анализа. Рекомендуемая форма изложения приведена в приложении Б.
4.13 При применении методик анализа с установленными показателями качества в конкретной лаборатории оценивают и контролируют внутрилабораторную прецизионность анализа и систематическую погрешность лаборатории. Нормативы внутрилабораторного контроля устанавливают с учетом приписанной характеристики погрешности (ее составляющих), нормативы внешнего контроля - на ее основе.
Примечание - Оценки внутрилабораторной прецизионности и систематической погрешности лаборатории могут быть проведены с использованием алгоритмов, изложенных в настоящих рекомендациях, при их реализации (алгоритмов) в конкретной лаборатории, а также на основе рекомендаций [1] - [5].
5 Исходная модель
5.1 В соответствии с разделом 5 [1] и разделом 4 [4] при оценке показателей качества методики анализа каждый результат единичного анализа X и приписанная характеристика его погрешности D могут быть представлены в виде:
Х = С + Dс + DLс + ![]() r, (1)
r, (1)
D = Dс + DLс + ![]() r, (2)
r, (2)
где С - истинное [или в его отсутствие принятое опорное (по 3.22, перечисления а), б), в)] значение;
Dс - оценка систематической погрешности методики анализа;
DLс - оценка лабораторной составляющей систематической погрешности, формирующей межлабораторную вариацию;
![]() r
- оценка случайной погрешности результата единичного анализа, полученного в
условиях повторяемости.
r
- оценка случайной погрешности результата единичного анализа, полученного в
условиях повторяемости.
Примечание - Описание составляющих погрешности каждого результата анализа приведено в приложении В.
5.2 В соответствии с разделом 5 [1] в случае, когда в качестве опорного значения принято математическое ожидание измеряемой характеристики, то есть среднее значение заданной совокупности результатов анализа [3.22, перечисление г)], каждый результат единичного анализа X и приписанная характеристика его погрешности D могут быть представлены в виде:
Х = ![]() + DLс +
+ DLс + ![]() r, (3)
r, (3)
D = DLс + ![]() r, (4)
r, (4)
где ![]() - общее среднее
(оценка математического ожидания) результатов анализа, полученных в условиях
воспроизводимости;
- общее среднее
(оценка математического ожидания) результатов анализа, полученных в условиях
воспроизводимости;
DLс - оценка лабораторной составляющей систематической погрешности;
![]() r
- оценка случайной погрешности результата единичного
анализа, полученного в условиях повторяемости.
r
- оценка случайной погрешности результата единичного
анализа, полученного в условиях повторяемости.
5.3 Для каждого из результатов анализа - ![]() , полученного по методике с установленными
показателями качества, допустима следующая форма представления:
, полученного по методике с установленными
показателями качества, допустима следующая форма представления:
![]() ± D, Р.
± D, Р.
Примечание - Величину D принимают в качестве приписанной характеристики погрешности методики анализа и приводят в документе на методику анализа, в свидетельстве об аттестации методики анализа, а также используют при оценке лабораторий на качество проведения испытаний.
В протоколах испытаний, оформляемых при реализации методики анализа с установленными показателями качества в конкретной лаборатории, более предпочтительной является следующая форма представления результата анализа:
![]() ± Dл, Р.
± Dл, Р.
где Dл - характеристика погрешности любого из совокупности результатов анализа, полученного в данной лаборатории при реализации методики анализа (рассчитанная с учетом внутрилабораторной прецизионности и обеспечиваемая процедурами внутрилабораторного контроля).
6 Метод оценки показателей качества методики анализа с помощью набора образцов для оценивания в виде СО или АС в условиях получения экспериментальных данных в нескольких лабораториях
6.1 Основные допущения и общие требования к проведению эксперимента
6.1.1 Распределение случайной погрешности результата анализа принимают нормальным1).
6.1.2 Распределение неисключенной систематической погрешности методики анализа принимают нормальным.
6.1.3 Распределение погрешности аттестации образцов для оценивания принимают равномерным.
6.1.4 Влияющие факторы пробы не оказывают значимого влияния на погрешность результата анализа.
6.1.5 Образцы для оценивания (ОО) выбирают таким образом, чтобы содержание определяемого компонента в ОО позволило охватить диапазон измерений, предусмотренных методикой анализа.
6.1.6 Общий состав ОО должен соответствовать области применения методики анализа.
6.1.7 В общем случае число ОО должно быть не менее пяти.
Примечание - Если в процессе разработки методики установлено отсутствие значимой зависимости погрешности результатов анализа, выполняемых по методике анализа, от измеряемого содержания (например, небольшой диапазон измерений) или получена информация о линейной зависимости погрешности от измеряемого содержания, то допустимо использование одного или двух ОО соответственно.
6.1.8 ОО должны быть стабильны во время проведения эксперимента. В противном случае нестабильность ОО будет одним из факторов, формирующих прецизионность анализа. Общие требования к стабильности ОО приведены в [1], [2].
6.1.9 ОО должны быть выбраны таким образом, чтобы погрешность, связанная с изменением содержания компонента в навесках этого ОО, была пренебрежимо мала по сравнению с показателем повторяемости методики анализа, в противном случае она будет одним из факторов, формирующих прецизионность анализа.
6.1.10 Планирование эксперимента должно отвечать условиям воспроизводимости. С этой целью ОО отсылают в L лабораторий, каждая из которых получает N результатов единичного анализа в условиях повторяемости. Выбор числа лабораторий и числа результатов единичного анализа каждого ОО осуществляют в соответствии с приложением Г и [1], [2], [4]. При выборе числа лабораторий и результатов единичного анализа необходимо учитывать погрешность оценки среднего квадратического отклонения воспроизводимости.
Примечание - В соответствии с [2] под «лабораторией» подразумевают сочетание таких факторов, как «оператор», «оборудование» и «место измерений». Одна лаборатория в общепринятом значении этого слова представляет собой несколько «лабораторий» в том случае, если она может предусматривать наличие нескольких операторов, каждый из которых располагает своим рабочим местом с комплектом оборудования и условиями, в которых выполняют работу.
6.1.11 Получение результатов единичного анализа с учетом [2] организуют с соблюдением следующих рекомендаций:
а) применяют поверенные (калиброванные) средства измерений;
б) каждую группу из N1) результатов единичного анализа получают при соблюдении условий повторяемости, т.е. в пределах короткого интервала времени, с помощью одного и того же оператора, с использованием одной и той же мерной посуды, одних и тех же партий реактивов одного типа, одних и тех же средств измерений;
в) в каждой лаборатории единичные анализы выполняют в соответствии с процедурой, описанной в методике анализа, независимым образом так, как если бы это были N результатов единичного анализа различных проб;
г) группы из N результатов единичного анализа разных ОО в одной лаборатории могут быть получены в разные дни, но обязательно одним оператором. Если один оператор не может выполнить анализы всех ОО, допускается его замена другим оператором при анализе другого ОО, при этом N результатов единичного анализа одного ОО должны быть получены одним оператором;
д) форма представления результатов единичного анализа каждого ОО - в соответствии с приложением Д.
1) Число результатов параллельных определений, получаемых в соответствии с прописью методики, обозначено п.
В каждой лаборатории назначают ответственного за организацию фактического выполнения эксперимента.
Примечание к 6.1.11 и 6.1.12 - При организации проведения эксперимента по оценке показателей качества конкретной методики анализа подлежат учету рекомендации, данные в приложении Г.
6.1.13 Экспериментальные данные, полученные из лабораторий, представляют в виде таблицы 2.
Таблица 2 - Результаты единичного анализа образцов для оценивания
|
(m = ) |
Содержание определяемого компонента в ОО (аттестованное значение ОО) Ст |
Погрешность аттестованного значения ОО Dот |
Номер лаборатории (l = ) |
Номер результата единичного анализа,
полученного в условиях повторяемости (I = |
||||
|
1 |
... |
i |
... |
N |
||||
|
1 |
C1 |
Do1 |
1 ... L |
X111 ... X1L1 |
... ... ... |
X11i ... X1Li |
... ... ... |
X11N ... X1LN |
|
... |
... |
... |
... |
... |
... |
... |
... |
... |
|
т |
ст |
Dот |
1 ... l ... L |
Xm11 ... Xml1 ... XmL1 |
... ... ... ... ... |
Xm1i ... Xmli ... XmLi |
... ... ... ... ... |
Xm1N ... XmlN ... XmLN |
|
... |
... |
... |
... |
... |
... |
... |
... |
... |
|
M |
См |
DоM |
1 ... L |
XM11 ... XML1 |
... ... ... |
XM1i ... XMLi |
... ... ... |
XM1N ... XMLN |
6.1.14 Если методику анализа разрабатывают для ее применения в одной лаборатории, экспериментальные данные получают в этой лаборатории, варьируя всеми факторами, формирующими промежуточную (внутрилабораторную) прецизионность (серии результатов единичного анализа получают в разное время, разные операторы, используя разные партии реактивов одного типа, разные наборы мерной посуды и т.п.). Результаты единичного анализа внутри каждой серии получают в одинаковых условиях и практически одновременно. При этом число серий результатов единичного анализа выбирают с учетом рекомендаций 6.1.10 для числа лабораторий при организации межлабораторного эксперимента. Время проведения эксперимента занимает период, охватывающий такие изменения, как градуировка средств измерений, смена реактивов одного типа, изменение условий окружающей среды и т.д.
6.2 Оценка показателей прецизионности (повторяемости и воспроизводимости) методики анализа
6.2.1 Оценка показателя повторяемости методики анализа
6.2.1.1 Рассчитывают среднее арифметическое Хтl и выборочную дисперсию S2ml результатов единичного анализа содержания компонента в m-м ОО, полученных в условиях повторяемости (параллельных определений):
 (5)
(5)
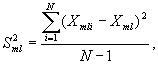 (6)
(6)
т = 1, ..., M; l = 1, ..., L.
6.2.1.2 На основе полученных значений выборочных дисперсий S2ml ..., S2mL в т-м ОО проверяют гипотезу о равенстве генеральных дисперсий1), используя критерий Кохрена.
1) Дисперсии результатов единичного анализа, полученные в различных лабораториях, имеют различные значения. Предполагают, что для аттестованной методики анализа такие различия между лабораториями невелики и что допустимо установить одно общее (усредненное) значение дисперсии для всех лабораторий, применяющих данную методику.
Значение критерия Кохрена Gm (max) рассчитывают по формуле
 (7)
(7)
и сравнивают его с табличным значением этого критерия Gтабл для числа степеней свободы v = N - 1, соответствующего максимальной дисперсии, и f = L, соответствующего числу суммируемых дисперсий, и принятой доверительной вероятности Р = 0,95 (значения Gтабл приведены в приложении Е, таблица Е.1). Если Gm(max) > Gтабл, то соответствующее (S2ml)max из дальнейших расчетов исключают и процедуру повторяют до следующего по значению S2ml и т.д. до тех пор, пока Gm(max) не станет меньше либо равно Gтабл.
6.2.1.3 Не исключенные из расчетов S2ml считают однородными и по ним оценивают средние квадратические отклонения (далее - СКО), характеризующие повторяемость результатов единичного анализа (параллельных определений), полученных для содержания, соответствующего содержанию компонента в m-м OO. Эти СКО - Srm рассчитывают по формуле
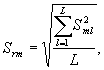 (8)
(8)
где в числе слагаемых нет отброшенных значений.
6.2.1.4 Показатель повторяемости методики анализа в виде СКО1) - srm для содержания, соответствующего содержанию компонента в m-м ОО, устанавливают, принимая равным Srm
srm ≈ Srm 9)
1) Стандартное отклонение повторяемости по [1].
6.2.1.5 Показатель повторяемости методики анализа в виде предела повторяемости2) - rnm для содержания, соответствующего содержанию компонента в m-м ОО, рассчитывают по формуле
rnm = Q(Р, п)srm, (10)
где п - число параллельных определений, предусмотренных методикой анализа для получения результата анализа,
Q(P, п) = 2,77 при п = 2, Р = 0,95;
Q(P, п) = 3,31 при п = 3, Р = 0,95;
Q(P, п) = 3,63 при п = 4, Р = 0,95;
Q(P, п) = 3,86 при п = 5, Р = 0,95.
2) Значение предела повторяемости рассчитывают в случае, если методикой анализа предусмотрено проведение параллельных определений, и используют при проверке приемлемости результатов единичного анализа, полученных в условиях повторяемости.
6.2.2 Оценка показателя воспроизводимости методики анализа
6.2.2.1 Рассчитывают выборочное СКО результатов анализа m-го OO, полученных в условиях воспроизводимости, - SRm по формуле
 (11)
(11)
где Хт - общее среднее значение результатов анализа, полученных в условиях воспроизводимости.
Хт рассчитывают по формуле
 (12)
(12)
Примечание - В случае, если методикой анализа не предусмотрено проведение параллельных определений (n = 1) и результат единичного анализа является собственно результатом анализа, выборочное СКО результатов анализа m-го OO, полученных в условиях воспроизводимости, рассчитывают по формуле
 (13)
(13)
6.2.2.2 Оценка показателя воспроизводимости методики анализа
Показатель воспроизводимости методики анализа в виде СКО1) - sRm для содержания, соответствующего содержанию компонента в т-м OO, устанавливают, принимая равным SRm:
sRm ≈ SRm. (14)
1) Стандартное отклонение воспроизводимости по [1].
Показатель воспроизводимости методики анализа в виде предела воспроизводимости2) - Rm для содержания, соответствующего содержанию компонента в т-м ОО, рассчитывают по формуле
![]()
Rm = Q(P, 2)sRm, (15)
где Q(P, 2) = 2,77 при Р = 0,95.
2) Значение предела воспроизводимости используют при проверке приемлемости результатов анализа, полученных в условиях воспроизводимости.
Примечание - В случае невозможности организации эксперимента в разных лабораториях экспериментальные данные получают в одной лаборатории в условиях внутрилабораторной прецизионности (серии результатов единичного анализа получают в разное время, разные операторы, используя разные партии реактивов одного типа, разные наборы мерной посуды и т.п.). Результаты единичного анализа внутри каждой серии получают в условиях повторяемости. В этом случае показатель воспроизводимости методики анализа в виде СКО рассчитывают по формуле
sRm ≈ kS![]() m, (16)
m, (16)
где S![]() m -
выборочное СКО результатов анализа, рассчитанное в соответствии с 6.2.2.1 на основе результатов, полученных в условиях
внутрилабораторной прецизионности;
m -
выборочное СКО результатов анализа, рассчитанное в соответствии с 6.2.2.1 на основе результатов, полученных в условиях
внутрилабораторной прецизионности;
k - коэффициент, учитывающий условия проведения эксперимента. k может принимать значения от 1,2 до 2,0.
6.3 Оценка показателя правильности методики анализа
6.3.1 Рассчитывают оценку математического ожидания систематической погрешности методики анализа - Θm как разность между средним значением результатов анализа Хт и аттестованным значением m-го OO (СО или АС) - Сm
Θm = Хm - Ст, т = 1, ..., М. (17)
6.3.2 Проверяют значимость вычисленных значений Θm по критерию Стьюдента. Для этого рассчитывают значение t-критерия для т-го OO - tm:
 (18)
(18)
где ![]()
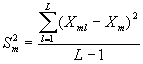 - дисперсия,
характеризующая разброс средних арифметических значений результатов единичного
анализа Хтl, полученных в l-й
лаборатории, относительного среднего значения результатов анализа Хт;
- дисперсия,
характеризующая разброс средних арифметических значений результатов единичного
анализа Хтl, полученных в l-й
лаборатории, относительного среднего значения результатов анализа Хт;
Dот - погрешность аттестованного значения т-го OO.
6.3.3 Полученное значение tm сравнивают с tтабл при числе степеней свободы f = L - 1 для доверительной вероятности Р = 0,95. Значения tтабл приведены в приложении Е, таблица Е.2.
6.3.4 Если tm £ tтабл, то оценка систематической погрешности незначима на фоне случайного разброса, и в этом случае ее принимают равной нулю (Θm = 0).
6.3.5 Если tm > tтабл, то оценка систематической погрешности значима на фоне случайного разброса и для принятия решения о приемлемости методики анализа вводят еще один дополнительный критерий:
|Θm| £ ξsRm,
где ξ может принимать значения от 0,5 до 1 в зависимости от используемых в методике анализа метода, условий, средств измерений и т.п., а также характеристик объекта анализа.
При выполнении данного критерия может быть принято решение (с учетом примечания к 6.4) о введении в результаты анализа, получаемые при реализации данной методики, поправки на значение Θ, т.е. значение Θ, соответствующее содержанию С - Θ (С), вычитают из любого результата анализа, полученного по методике.
Если данный критерий не выполняется, принимают решение о доработке методики.
6.3.6 При незначимости Θ или при принятом для методики анализа решении о введении в результаты анализа поправки показатель правильности методики анализа [верхнюю (Dс.в т) и нижнюю (Dс.н т) границы, в которых неисключенная систематическая погрешность методики анализа (для содержания, соответствующего содержанию определяемого компонента в т-м ОО) находится с принятой вероятностью Р = 0,95] рассчитывают по формуле
Dс.в т = |Dс.н т| = Dc m
= 1,961) ![]() (19)
(19)
Примечание - При условии организации эксперимента согласно примечанию к 6.2.2.2 показатель правильности методики анализа (границы, в которых неисключенная систематическая погрешность методики анализа находится с принятой вероятностью Р = 0,95) рассчитывают по формуле
Dс.в т = |Dс.н т| = Dc m = 1,961) ![]() (20)
(20)
где Sл т - выборочное СКО результатов анализа, рассчитанное в соответствии с 6.3.2 на основе результатов, полученных в условиях внутрилабораторной прецизионности;
k - коэффициент, учитывающий условия проведения эксперимента. k может принимать значения от 1,2 до 2,0.
1) Используют квантиль для нормального распределения в связи с близостью суперпозиционного распределения к нормальному [8].
6.4 Оценка показателя точности методики анализа
Верхнюю (Dв т) и нижнюю (Dн т) границы, в которых погрешность результата анализа2) (для содержания, соответствующего содержанию определяемого компонента в m-м OO) находится с принятой вероятностью Р = 0,95, рассчитывают по формуле
Dв т = |Dн т| = Dm = 1,96 ![]() (21)
(21)
2) При незначимости Θ или при принятии решения о введении поправки в результат анализа.
Примечания
1 Здесь и
далее: при выполнении условия ![]() < 0,8показатель точности методики анализа
может быть рассчитан по формуле
< 0,8показатель точности методики анализа
может быть рассчитан по формуле
Dв(н) т = ±1,96 sRm. (22)
2 В случае, если учет Θ (С) при вычислении показателя правильности методики анализа
Dc.в(н) т = Θm ±1,96 sc т, (23)
где Dc.в(н) т - верхняя и нижняя границы, в которых систематическая погрешность методики анализа находится с принятой вероятностью Р = 0,95, не приводит к превышению приписанной характеристики погрешности результата анализа над нормой погрешности, поправку в результат на значение Θ (С) можно не вносить.
В этом случае показатель точности методики анализа (для содержания, соответствующего содержанию определяемого компонента в т-м OO) рассчитывают по формуле
Dв(н) т = Θm ± 1,96 sт (D). (24)
6.5 Установление показателя точности во всем диапазоне действия методики анализа
6.5.1 Устанавливают функциональную зависимость приписанной характеристики погрешности результатов анализа от содержания определяемого компонента по значениям Dт, Ст (т = 1, ..., М), проверяя при этом с использованием статистических критериев (например, r*-критерия [9]) адекватность устанавливаемой зависимости экспериментальным данным (Dт, Сm)1).
1) Возможные виды зависимости и формулы расчета оценок коэффициентов этих зависимостей приведены в приложении Ж.
Так, если установлена линейная зависимость приписанной характеристики погрешности от содержания определяемого компонента, то для расчета приписанной характеристики погрешности результатов анализа в любой точке диапазона, предусмотренного методикой анализа, используют выражение
Dв(С) + |Dн(С)| = D(С) = a1 + a2С, (25)
где параметры a1 и a2 могут быть найдены методом наименьших квадратов2).
2) В случае, если оценки погрешности не являются равноточными, целесообразнее использовать взвешенный метод наименьших квадратов.
6.5.2 Диапазон действия методики анализа (для практического удобства использования значений показателей качества методики анализа) может быть разбит на поддиапазоны, в пределах которых изменением значений показателей качества методики анализа в зависимости от содержания можно пренебречь. Разбивку на поддиапазоны осуществляют на основе показателя воспроизводимости - sRm. Для этого определяют во всем диапазоне измерений вид зависимости sRm от Ст аналогично 6.5.1. Устанавливают границы поддиапазонов, для которых значения sR, соответствующие верхней и нижней границам поддиапазона, можно признать однородными, т.е. отношение максимальной дисперсии к минимальной не превышает двух. На основе установленного вида зависимости D(С) определяют значения D, соответствующие серединам поддиапазонов, на которые был разбит весь диапазон измерений (по значениям sR). Найденные значения D принимают постоянными в пределах установленных поддиапазонов.
6.5.3 Если оценку приписанной характеристики случайной погрешности результатов анализа проводили с использованием рабочих проб, то необходимое число образцов для оценивания приписанной характеристики систематической погрешности устанавливают с учетом числа поддиапазонов, на которые разбивают диапазон действия методики анализа (по значениям sR).
6.5.4 При отсутствии выявляемой зависимости sRm от Ст устанавливают одно значение показателя воспроизводимости для всего диапазона. В этом случае для оценки показателя правильности допустимо использование одного образца для оценивания.
7 Метод оценки показателей качества методики анализа с применением однофакторных планов эксперимента
7.1 Основные допущения
7.1.1 Распределение случайной погрешности результата анализа принимают нормальным.
7.1.2 Применение метода однофакторных экспериментов позволяет оценить приписанную характеристику систематической погрешности методики анализа при наличии влияющих факторов пробы.
7.1.3 Систематическая погрешность методики анализа формируется из неисключенных остатков постоянной части Θo и варьируемой части Θв, обусловленной влияющими факторами пробы.
Приписанную характеристику неисключенной систематической погрешности методики анализа находят с использованием закона равномерного распределения ее составляющих.
7.1.4 Распределение погрешности аттестации образцов для оценивания принимают равномерным.
7.2 Оценка показателей прецизионности (повторяемости и воспроизводимости) методики анализа
7.2.1 Оценка показателей повторяемости и воспроизводимости методики анализа может быть проведена на рабочих пробах, СО или АС. Общие требования к организации эксперимента и методы оценки аналогичны рассмотренным в 6.1 - 6.2.
7.2.2 На основе установленной зависимости sR от содержания определяемого компонента с учетом 6.5.2 диапазон измерений разбивают на поддиапазоны, в пределах которых можно принять постоянство sR.
7.3 Требования к образцам для оценки показателя правильности методики анализа
7.3.1 Для учета влияния каждого j-го влияющего фактора пробы необходимо иметь два ОО (СО или АС) для каждого из поддиапазонов с принятым значением sRm (т = 1, ..., М). Для каждой пары образцов содержание определяемого компонента должно быть одно и то же, а значение j-го влияющего фактора должно находиться в одном образце вблизи нижней границы его возможных значений, а в другом - вблизи верхней. Значения других влияющих факторов должны быть одними и теми же.
7.3.2 Организация проведения эксперимента по оценке показателя правильности конкретной методики анализа должна быть осуществлена в соответствии с 6.1.11 и 6.1.12 и приложением Г. В общем случае для каждого из т поддиапазонов для каждого j-го влияющего фактора в соответствии с требованиями методики анализа получают L результатов анализа, максимально варьируя при этом условия проведения анализа: разные лаборатории, разное время, разные операторы, разные наборы мерной посуды и т.п.
Число L результатов анализа выбирают в соответствии с приложением Г и [4] в зависимости от возможной неопределенности оценки систематической погрешности методики анализа.
Примечание - Если методикой анализа предусмотрено выполнение параллельных определений для получения результата анализа, то хнjl и хвjl представляют собой результаты анализа, средние арифметические результатов параллельных определений.
Экспериментальные данные представляют в виде таблицы 3 (для каждого j-го влияющего фактора - своя таблица).
Таблица 3 - Состав ОО и результаты анализа ОО
|
Аттестованное значение ОО Ст |
Погрешность аттестованного значения ОО Dот |
Состав образцов (значение j-го влияющего фактора) |
Номер результата анализа |
||
|
1 |
... |
L |
|||
|
C1 |
Do1 |
Вблизи нижней границы диапазона |
хнj11 |
... |
хнj1L |
|
Вблизи верхней границы диапазона |
хвj11 |
... |
хвj1L |
||
|
... |
... |
... |
|
... |
... |
|
См |
DoM |
Вблизи нижней границы диапазона |
хнjM1 |
... |
хнjML |
|
Вблизи верхней границы диапазона |
хвjM1 |
... |
хвjML |
||
7.4 Оценка показателя правильности методики анализа
7.4.1 Для каждой m-й точки диапазона действия методики анализа, соответствующей содержанию определяемого компонента в ОО, рассчитывают
 - среднее
арифметическое значение L
результатов анализа ОО с содержанием j-го
влияющего фактора вблизи его нижней границы; (26)
- среднее
арифметическое значение L
результатов анализа ОО с содержанием j-го
влияющего фактора вблизи его нижней границы; (26)
 - среднее значение L результатов
анализа ОО с содержанием j-го влияющего фактора вблизи его верхней
границы; (27)
- среднее значение L результатов
анализа ОО с содержанием j-го влияющего фактора вблизи его верхней
границы; (27)
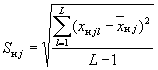 - CKO, характеризующее
случайный разброс результатов анализа хн j1, ..., хн jL; (28)
- CKO, характеризующее
случайный разброс результатов анализа хн j1, ..., хн jL; (28)
 - CKO, характеризующее
случайный разброс результатов анализа хв j1, ..., хв jL. (29)
- CKO, характеризующее
случайный разброс результатов анализа хв j1, ..., хв jL. (29)
7.4.2 Границы, в которых с принятой вероятностью Р = 0,95 находится составляющая систематической погрешности методики анализа, обусловленная влиянием j-го фактора пробы, рассчитывают по формулам (для поддиапазона т):
 (30)
(30)
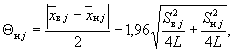 (31)
(31)
За эффект влияния j-го фактора Θj принимают величину Θв j.
Примечание - Если число влияющих факторов J > 1, то составляющую систематической погрешности методики анализа, обусловленную влияющими факторами пробы, рассчитывают по формуле
 (32)
(32)
где J - число влияющих факторов пробы. При J = 1 Θв = Θj.
7.4.3 Характеристику постоянной части систематической погрешности методики анализа устанавливают, рассчитывая (для поддиапазона т)
![]() - среднее арифметическое
результатов анализа ОО с содержанием С (для данного поддиапазона
т; при J
> 1 расчеты выполняют по любой паре образцов); (33)
- среднее арифметическое
результатов анализа ОО с содержанием С (для данного поддиапазона
т; при J
> 1 расчеты выполняют по любой паре образцов); (33)
Θ = ![]() - C - оценку математического ожидания постоянной части систематической
погрешности методики анализа; (34)
- C - оценку математического ожидания постоянной части систематической
погрешности методики анализа; (34)
 (35)
(35)
где Do - погрешность ОО.
7.4.4 Полученное значение t сравнивают с tтабл при числе степеней свободы f = L - 1. Значения tтабл приведены в приложении Е, таблица Е.2.
7.4.5 Если t £ tтабл, то оценка постоянной части систематической погрешности незначима на фоне случайного разброса и в этом случае ее принимают равной нулю (Θ = 0).
7.4.6 Если t > tтабл, то оценка постоянной части систематической погрешности значима на фоне случайного разброса и для принятия решения о приемлемости методики анализа вводят еще один критерий:
|Θ| £ ξsR,
где ξ может принимать значения от 0,5 до 1 в зависимости от используемых в методике метода, условий, средств измерений и т.п., а также характеристик объекта анализа.
При выполнении данного критерия принимают решение о введении в результаты анализа, получаемые при реализации данной методики, поправки на значение Θ с учетом рекомендаций 6.3.5.
Если данный критерий не выполняется, принимают решение о доработке методики.
7.4.7 Показатель правильности методики анализа (границы, в которых с принятой вероятностью Р = 0,95 находится систематическая погрешность методики анализа) рассчитывают по формуле (для поддиапазона т)
Dс.в = |Dс.н| = Dc = 1,1![]() (36)
(36)
где Θo - границы, в которых с принятой вероятностью Р = 0,95 находятся неисключенные остатки постоянной части систематической погрешности,
Θo = Θoв
= |Θoн| = 1,96 (37)
(37)
Примечание - В случае невозможности организации эксперимента в разных лабораториях экспериментальные данные получают в одной лаборатории в условиях внутрилабораторной прецизионности (серии результатов единичного анализа получают в разное время, разные операторы, используя разные партии реактивов одного типа, разные наборы мерной посуды и т.п.). Результаты единичного анализа внутри каждой серии получают в условиях повторяемости. В этом случае составляющую систематической погрешности методики анализа, обусловленную влияющими факторами пробы, и характеристику постоянной части систематической погрешности методики анализа рассчитывают по формулам:
![]() (38)
(38)
Θoв
= |Θoн|
= Θo
= 1,96![]() (39)
(39)
где Sл.в j, Sл.н j - СКО результатов анализа, рассчитанные в соответствии с 7.4.1 на основе результатов, полученных в условиях внутрилабораторной прецизионности;
k - коэффициент, учитывающий условия проведения эксперимента. k может принимать значения от 1,2 до 2,0.
7.5 Оценка показателя точности методики анализа (для содержания, соответствующего содержанию определяемого компонента в ОО в поддиапазоне т)
7.5.1 Верхнюю (Dв) и нижнюю (Dн) границы, в которых погрешность результата анализа находится с принятой вероятностью Р = 0,95, рассчитывают по формуле
 (40)
(40)
7.5.2 При необходимости по найденным для каждого из поддиапазонов значениям D устанавливают функциональную зависимость D от содержания определяемого компонента для всего диапазона действия методики анализа с учетом рекомендаций 6.5.
8 Метод оценки показателей качества методики анализа с применением методики с известными (оцененными) характеристиками погрешности (методики сравнения)
8.1 Основные допущения
8.1.1 Распределение случайной погрешности результатов анализа, получаемых по методике, показатели качества которой оценивают (далее - исследуемая методика), принимают нормальным.
8.1.2 Распределение неисключенной систематической погрешности исследуемой методики принимают нормальным.
8.1.3 Влияющие факторы пробы не оказывают значимого влияния на погрешность результата анализа, выполняемого по исследуемой методике.
8.1.4 Область применения методики сравнения совпадает с областью применения исследуемой методики или перекрывает ее.
8.1.5 Значение показателя воспроизводимости методики сравнения не превышает значения показателя воспроизводимости исследуемой методики. При этом дисперсии воспроизводимости результатов анализа, получаемых по обеим методикам, должны быть однородны.
8.1.6 Систематическая погрешность методики сравнения незначима на фоне ее случайной погрешности.
8.1.7 Распределение погрешности результатов анализа, получаемых по методике сравнения, принимают нормальным.
8.1.8 Методика сравнения должна удовлетворять требованиям внутрилабораторного контроля точности ее результатов.
8.2 Оценка показателей прецизионности (повторяемости и воспроизводимости) исследуемой методики анализа
8.2.1 Оценка показателей повторяемости и воспроизводимости исследуемой методики анализа может быть проведена с использованием рабочих проб1). Общие требования к организации эксперимента и методы оценки аналогичны рассмотренным в 6.1 - 6.2.
8.2.2 На основе установленной зависимости sR от содержания определяемого компонента с учетом 6.5.2 диапазон измерений разбивают на поддиапазоны, в пределах которых можно принять постоянство sR.
8.3 Оценка показателя правильности методики анализа
8.3.1 Показатель правильности исследуемой методики анализа оценивают в каждом интервале (поддиапазоне) содержания определяемого компонента, для которого установлено постоянство показателей воспроизводимости исследуемой методики и методики сравнения.
8.3.2 Для оценки показателя правильности исследуемой методики в каждом поддиапазоне используют не менее одной пробы анализируемого вещества (материала) с содержанием определяемого компонента, соответствующим данному поддиапазону.
8.3.3 Организация проведения эксперимента по оценке показателя правильности исследуемой методики анализа должна быть осуществлена в соответствии с 6.1.11, 6.1.12 и приложением Г.
В общем случае для каждого из т поддиапазонов в соответствии с требованиями исследуемой методики и методики сравнения получают по L результатов анализа, максимально варьируя при этом условия проведения анализа: разные лаборатории, разное время, разные операторы, разные наборы мерной посуды и т.п.
Анализ одной и той же пробы по исследуемой методике и методике сравнения проводят в одинаковых условиях, причем число L результатов анализа одной пробы, выполненных по исследуемой методике и методике сравнения, должно совпадать.
Число L результатов анализа выбирают в соответствии с приложением Г и [4] в зависимости от возможной неопределенности оценки систематической погрешности исследуемой методики анализа.
Полученные результаты представляют в виде таблицы 4.
Примечание - Если исследуемой методикой анализа и (или) методикой сравнения предусмотрено выполнение параллельных определений для получения результата анализа, то хl и (или) xcl представляют собой результаты анализа, средние из результатов параллельных определений.
Θl = хl - xcl, l = 1, ..., L, (41)
где хl и xcl - результаты анализа проб, полученные по исследуемой методике и методике сравнения соответственно.
Полученные значения Θl вносят в таблицу 4.
 (42)
(42)
![]() (43)
(43)
8.3.6 Проверяют значимость расхождения результатов анализа, полученных по исследуемой методике и методике сравнения, по t-критерию. Для этого рассчитывают значение t
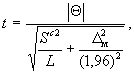 (44)
(44)
где Dм - установленная характеристика погрешности результатов анализа, полученных при соблюдении требований и правил методики сравнения, и сравнивают полученное значение t с tтабл при числе степеней свободы f = L - 1 для доверительной вероятности Р = 0,95. Значения tтабл приведены в приложении Е, таблица Е.2.
Таблица 4 - Результаты анализа рабочих проб, полученные по исследуемой методике и методике сравнения
|
Результаты анализа по исследуемой методике xl |
Результаты анализа по методике сравнения xcl |
Θl |
|
|
1 |
x1 |
xc1 |
Θ1 |
|
... |
... |
... |
|
|
l |
xl |
xcl |
Θl |
|
... |
... |
... |
... |
|
L |
xL |
xcL |
ΘL |
8.3.7 Если t £ tтабл, то делают вывод о незначимости расхождения результатов анализа, выполняемых по обеим методикам. В этом случае Θ принимают равным нулю (Θ = 0).
8.3.8 Если t > tтабл, то делают вывод о значимости расхождения результатов анализа и для принятия решения о приемлемости методики анализа вводят еще один критерий:
|Θ| £ ξsR,
где ξ может принимать значения от 0,5 до 1 в зависимости от используемых в методике метода, условий, средств измерений и т.п., а также характеристик объекта анализа.
При выполнении данного критерия может быть принято решение (с учетом примечания к 8.4.1) о введении в результаты анализа, получаемые при реализации данной методики, поправки на значение Θ (аналогично 6.3.5).
Если данный критерий не выполняется, принимают решение о доработке методики.
8.3.9 При незначимости Θ или при принятом для методики анализа решении о введении в результаты анализа поправки показатель правильности методики анализа - верхнюю (Dс.в) и нижнюю (Dс.н) границы, в которых неисключенная систематическая погрешность методики анализа находится с принятой вероятностью Р = 0,95, рассчитывают по формуле
Dс.в = |Dс.н| = Dc =  = 1,96 sc. (45)
= 1,96 sc. (45)
Примечание - В случае невозможности организации эксперимента в разных лабораториях экспериментальные данные получают в одной лаборатории в условиях внутрилабораторной прецизионности (серии результатов единичного анализа получают в разное время, разные операторы, используя разные партии реактивов одного типа, разные наборы мерной посуды и т.п.). Результаты единичного анализа внутри каждой серии получают в условиях повторяемости. В этом случае показатель правильности методики анализа (границы, в которых неисключенная систематическая погрешность методики анализа находится с принятой вероятностью Р = 0,95) рассчитывают по формуле
 (46)
(46)
где
![]() - выборочное СКО
результатов анализа, рассчитанное в соответствии с 8.3.4 и 8.3.5
на основе результатов, полученных в условиях внутрилабораторной прецизионности;
- выборочное СКО
результатов анализа, рассчитанное в соответствии с 8.3.4 и 8.3.5
на основе результатов, полученных в условиях внутрилабораторной прецизионности;
k - коэффициент, учитывающий условия проведения эксперимента. k может принимать значения от 1,2 до 2,0.
8.4 Оценка показателя точности методики анализа
8.4.1 Верхнюю (Dв) и нижнюю (Dн) границы, в которых погрешность результата единичного анализа1) находится с принятой вероятностью Р = 0,95, рассчитывают по формуле
![]() (47)
(47)
1) При незначимости Θ или при принятии решения о введении поправки в результат анализа.
Примечание - В случае, если учет Θ(C) при вычислении показателя правильности методики анализа
Dс.в(н) = Θ ± 1,96sс, (48)
где Dс.в(н) - верхняя и нижняя границы, в которых систематическая погрешность методики анализа находится с принятой вероятностью Р = 0,95, не приводит к превышению приписанной характеристики погрешности результата анализа над нормой погрешности, поправку в результат на значение Θ (С) можно не вносить.
В этом случае показатель точности методики анализа рассчитывают по формуле
Dв(н) = Θ ± 1,96s (D). (49)
8.4.2 При необходимости по найденным для каждого из поддиапазонов значениям D устанавливают функциональную зависимость D от содержания определяемого компонента для всего диапазона действия методики анализа с учетом рекомендаций 6.5.
9 Метод оценки показателей качества методики анализа с применением метода добавок
9.1 Основные допущения
9.1.1 Распределение случайной погрешности результатов анализа принимают нормальным.
9.1.2 Распределение неисключенной систематической погрешности методики анализа принимают нормальным.
9.1.3 Влияющие факторы пробы не оказывают значимого влияния на погрешность результата анализа.
9.1.4 Применение метода добавок позволяет провести оценивание мультипликативной (пропорционально изменяющейся) части систематической погрешности методики анализа.
Примечание - Использование способа допустимо, если на стадии предварительных исследований или по априорным данным установлено, что аддитивная (постоянная) часть систематической погрешности не является статистически значимой долей погрешности результата анализа.
9.1.5 Образцами для оценивания являются рабочие пробы вещества (материала) и рабочие пробы вещества (материала) с известной добавкой1). Специально приготовляемые пробы с известной добавкой должны быть однородными, соответствовать составу проб веществ (материалов), погрешность их приготовления не должна вносить дополнительную систематически значимую погрешность в приписанную характеристику систематической погрешности методики анализа. Содержание определяемого компонента в пробе с добавкой не превышает верхней границы поддиапазона, в котором принято постоянство показателя воспроизводимости sR. Наименьшие допускаемые значения добавки приведены в приложении И2).
1) В качестве добавки используют СО или АС.
2) Для методик, значение СКО воспроизводимости которых превышает 25 % содержания компонента в исходной пробе, применение метода добавок для оценки показателя правильности не рекомендуется.
9.1.6 Распределение погрешности аттестованного значения добавки является равномерным.
9.2 Оценка показателей прецизионности (повторяемости и воспроизводимости) методики анализа
9.2.1 Оценка показателей повторяемости и воспроизводимости методики анализа может быть проведена с использованием рабочих проб3). Общие требования к организации эксперимента и методы оценки аналогичны рассмотренным в 6.1 - 6.2.
3) При этом используемые пробы должны быть однородными и стабильными во все время проведения эксперимента. Подробнее - в [1].
9.2.2 На основе установленной зависимости sR от содержания определяемого компонента с учетом 6.5.2 диапазон измерений разбивают на поддиапазоны, в пределах которых можно принять постоянство sR.
9.3 Оценка показателя правильности методики анализа
9.3.1 Организация проведения эксперимента по оценке показателя правильности методики анализа должна быть осуществлена в соответствии с 6.1.11, 6.1.12 и приложением Г.
В общем случае необходимый для расчета массив экспериментальных данных для каждого m-го поддиапазона с принятым постоянным значением показателя воспроизводимости методики анализа получают в соответствии с методикой анализа в виде серии L результатов анализа определяемого компонента в пробе без добавки (х) и в пробе с добавкой (х’), максимально варьируя при этом условия проведения анализа: разные лаборатории, разное время, разные операторы, разные наборы мерной посуды и т.д.
Анализ пробы без добавки и пробы с добавкой проводят в одинаковых условиях, причем число L результатов анализа пробы и пробы с добавкой должно совпадать.
Выбор числа L результатов анализа осуществляют в соответствии с приложением Г и [4] в зависимости от возможной неопределенности оценки систематической погрешности методики анализа.
Экспериментальные данные представляют в виде таблицы 5.
Примечание - Если методикой анализа предусмотрено выполнение параллельных определений для получения результата анализа, то xl и х’l представляют собой результаты анализа, средние из результатов параллельных определений.
Таблица 5 - Результаты анализа пробы и пробы с добавкой при использовании метода добавок
|
Результаты анализа пробы без добавки хl |
Результаты анализа пробы с добавкой x'l |
Значение экспериментально найденной добавки xдl = x'l - xl |
|
|
1 |
x1 |
x'1 |
xд1 = x'1 - x1 |
|
... |
... |
... |
... |
|
l |
xl |
x'l |
xдl = x'l - xl |
|
... |
... |
... |
... |
|
L |
xL |
x'L |
xдL = x'L - xL |
9.3.2 Рассчитывают значения следующих величин:
 - среднее значение результатов
анализа пробы без добавки; (50)
- среднее значение результатов
анализа пробы без добавки; (50)
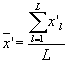 - среднее значение
результатов анализа пробы с добавкой; (51)
- среднее значение
результатов анализа пробы с добавкой; (51)
 - среднее значение
экспериментально найденной добавки; (52)
- среднее значение
экспериментально найденной добавки; (52)
 - СКО, характеризующее случайный разброс результатов анализа пробы
без добавки; (53)
- СКО, характеризующее случайный разброс результатов анализа пробы
без добавки; (53)
 - СКО, характеризующее случайный разброс результатов анализа пробы
с добавкой; (54)
- СКО, характеризующее случайный разброс результатов анализа пробы
с добавкой; (54)
Θ = ![]() - оценку
математического ожидания систематической погрешности методики анализа, где С
- аттестованное значение добавки к пробе; (55)
- оценку
математического ожидания систематической погрешности методики анализа, где С
- аттестованное значение добавки к пробе; (55)
 - рассчитанное значение t-критерия, (56)
- рассчитанное значение t-критерия, (56)
где Dдоб - погрешность аттестованного значения добавки к пробе.
9.3.3 Расчетное значение t сравнивают с tтабл при числе степеней свободы f = L - 1 и доверительной вероятности Р = 0,95 (значения tтабл приведены в приложении Е, таблица Е.2).
9.3.4 Если t £ tтабл, то оценка систематической погрешности незначима на фоне случайного разброса, и в этом случае ее принимают равной нулю (Θ = 0).
9.3.5 Если t > tтабл, то оценка систематической погрешности значима на фоне случайного разброса и для принятия решения о приемлемости методики анализа вводят еще один критерий:
|Θ| £ ξsR,
где ξ может принимать значения от 0,5 до 1 в зависимости от используемых в методике метода, условий, средств измерений и т.п., а также характеристик объекта анализа.
При выполнении данного критерия может быть принято решение (с учетом примечания к 9.4.1) о введении в результаты анализа, получаемые при реализации данной методики, поправки на значение Θ (аналогично 6.3.5).
Если данный критерий не выполняется, принимают решение о доработке методики.
9.3.6 При незначимости Θ или при принятом для методики анализа решении о введении в результаты анализа поправки показатель правильности методики анализа [верхнюю (Dс.в) и нижнюю (Dс.н) границы, в которых неисключенная систематическая погрешность методики анализа находится с принятой вероятностью Р = 0,95] рассчитывают по формуле
 (57)
(57)
Примечание - В случае невозможности организации эксперимента в разных лабораториях экспериментальные данные получают в одной лаборатории в условиях внутрилабораторной прецизионности (серии результатов единичного анализа получают в разное время, разные операторы, используя разные партии реактивов одного типа, разные наборы мерной посуды и т.п.). Результаты единичного анализа внутри каждой серии получают в условиях повторяемости. В этом случае показатель правильности методики анализа (границы, в которых не исключенная систематическая погрешность методики анализа находится с принятой вероятностью Р = 0,95) рассчитывают по формуле
 (58)
(58)
где Sл1, Sл2 - выборочные СКО результатов анализа пробы без добавки и пробы с добавкой, рассчитанные в соответствии с 9.3.2 на основе результатов, полученных в условиях внутрилабораторной прецизионности;
k - коэффициент, учитывающий условия проведения эксперимента. k может принимать значения от 1,2 до 2,0.
9.4 Оценка показателя точности методики анализа
9.4.1 Верхнюю (Dв) и нижнюю (Dн) границы, в которых погрешность результата анализа1) находится с принятой вероятностью Р = 0,95, рассчитывают по формуле
Dв = |Dн| = D
= 1,96![]() (59)
(59)
1) При незначимости Θ или при принятии решения о введении поправки в результат анализа.
Примечание - В случае, если учет Θ(С) при вычислении показателя правильности методики анализа
Dс.в(н) = Θ ± 1,96sс, (60)
где Dс.в(н) - верхняя и нижняя границы, в которых систематическая погрешность методики анализа находится с принятой вероятностью Р = 0,95, не приводит к превышению приписанной характеристики погрешности результата анализа над нормой погрешности, поправку в результат на значение Θ (С) можно не вносить.
В этом случае показатель точности методики анализа рассчитывают по формуле
Dв(н) = Θ ± 1,96s (D). (61)
9.4.2 При необходимости по найденным для каждого из поддиапазонов измерений значениям D устанавливают функциональную зависимость D от содержания определяемого компонента для всего диапазона измерений с учетом рекомендаций 6.5.
10 Метод оценки показателей качества методики анализа с применением метода добавок в сочетании с методом разбавления2)
10.1 Основные допущения
10.1.1 Распределение случайной погрешности результата анализа принимают нормальным.
10.1.2 Распределение неисключенной систематической погрешности методики анализа принимают нормальным.
10.1.3 Влияющие факторы пробы не оказывают значимого влияния на погрешность результата анализа.
10.1.4 Образцами для оценивания являются рабочие пробы вещества (материала), разбавленные рабочие пробы и разбавленные рабочие пробы с известной добавкой3). Специально приготовленные пробы (разбавленные пробы и разбавленные пробы с известной добавкой) должны быть однородными, соответствовать составу анализируемых проб, погрешность их приготовления не должна вносить дополнительную систематически значимую погрешность в приписанную характеристику систематической погрешности методики анализа.
3) В качестве добавки используют СО или АС.
10.1.5 Распределение погрешности аттестованного значения добавки и погрешности, обусловленной процедурой разбавления пробы, принимают равномерным.
10.2 Оценка показателей прецизионности (повторяемости и воспроизводимости) методики анализа
10.2.1 Оценка показателей повторяемости и воспроизводимости методики анализа может быть проведена с использованием рабочих проб1). Общие требования к организации эксперимента и методы оценки аналогичны рассмотренным в 6.1 - 6.2.
1) При этом используемые пробы должны быть однородными и стабильными во все время проведения эксперимента. Подробнее - в [1].
10.2.2 На основе установленной зависимости sR от содержания определяемого компонента с учетом 6.5.2 диапазон измерений разбивают на поддиапазоны, в пределах которых можно принять постоянство sR.
10.3 Оценка показателя правильности методики анализа
10.3.1 Организация проведения эксперимента по оценке показателя правильности конкретной методики анализа должна быть осуществлена в соответствии с 6.1.11, 6.1.12 и приложением Г.
В общем случае необходимый для расчета массив экспериментальных данных для каждого т-го поддиапазона с принятым постоянным значением показателя воспроизводимости методики анализа получают в соответствии с методикой анализа как серию L результатов анализа пробы (х), разбавленной пробы (x’р) и разбавленной пробы с добавкой (х"), максимально варьируя при этом условия проведения анализа: разные лаборатории, разное время, разные операторы, разные наборы мерной посуды и т.д. Анализ пробы, разбавленной пробы и разбавленной пробы с добавкой проводят в одинаковых условиях.
Число L результатов анализа выбирают в соответствии с приложением Г и [4] в зависимости от возможной неопределенности оценки систематической погрешности методики анализа.
При этом объем каждой отобранной пробы должен быть не менее 2L объема, необходимого для получения одного результата анализа (L - предполагаемое число результатов анализа одного OO). Каждую исходную пробу вещества (материала) делят на две равные части. Первую часть оставляют без изменения, а вторую разбавляют в η раз. Разбавленную пробу снова делят на две равные части, первую часть разбавленной пробы оставляют без изменения, а во вторую часть разбавленной пробы вводят добавку определяемого компонента. Наименьшие допускаемые значения добавки и кратности разбавления в зависимости от значения sR приведены в приложении И. При определении значения добавки и кратности разбавления обращают внимание на то, чтобы содержание компонента в пробе, разбавленной пробе и разбавленной пробе с добавкой находилось внутри поддиапазона постоянства sR2).
2) Для методик, значение СКО воспроизводимости которых превышает 25 % содержания компонента в исходной пробе, применение метода добавок в сочетании с методом разбавления не рекомендуется.
Экспериментальные данные представляют в виде таблицы 6.
Примечание - Если методикой анализа предусмотрено выполнение параллельных определений для получения результата анализа, то xl, х’p l и х"l представляют собой результаты анализа, средние из результатов параллельных определений.
Таблица 6 - Результаты анализа пробы, разбавленной пробы и разбавленной пробы с добавкой
|
Результаты анализа пробы xl |
Результаты анализа разбавленной пробы х’p l |
Результаты анализа разбавленной пробы с добавкой х"l |
|
|
1 |
x1 |
x’p1 |
x"1 |
|
... |
... |
... |
... |
|
l |
xl |
x’pl |
x"l |
|
... |
... |
... |
... |
|
L |
xL |
x’pL |
x"L |
10.3.2 Для каждого результата анализа рассчитывают:
- значения величин разности «введено - найдено» - Θlдоб и разности между результатами анализа определяемого компонента в рабочей пробе и разбавленной рабочей пробе с учетом кратности разбавления - Θlразб
Θlдоб = x"l - x’pl - Сввед, l = 1, ..., L, (62)
где Сввед - введенная добавка,
Θlразб = ηx’pl - xl; (63)
- средние арифметические значения разностей (Θlдоб, Θlразб, l = 1, ..., L)
Θдоб = 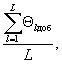 (64)
(64)
Θразб
=  (65)
(65)
- СКО разностей (Θlдоб, Θlразб, l = 1, ..., L)
 (66)
(66)
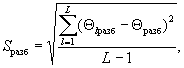 (67)
(67)
10.3.3 Определяют значимость полученных величин Θдоб и Θразб на фоне случайного разброса. Для этого рассчитывают
 (68)
(68)
 (69)
(69)
где Dдоб - погрешность аттестованного значения добавки;
Dразб - погрешность, обусловленная процедурой разбавления, которые сравнивают с tтабл для Р = 0,95 и числа степеней свободы f = L - 1. (Значения tтабл приведены в приложении Е, таблица Е.2)
Если tдоб £ tтабл (tразб £ tтабл), то соответствующее Θдоб (Θразб) незначимо на фоне случайного разброса и его исключают из дальнейших расчетов.
Если tдоб > tтабл (tразб > tтабл), то соответствующее Θдоб (Θразб) значимо на фоне случайного разброса и для принятия решения о приемлемости методики анализа вводят еще один критерий:
|Θдоб| £ ξsR, |Θразб| £ ξsR,
где ξ может принимать значения от 0,5 до 1 в зависимости от используемых в методике метода, условий, средств измерений и т.п., а также характеристик объекта анализа.
При выполнении данного критерия может быть принято решение (с учетом примечания к 10.4.1) о введении в результаты анализа, получаемые при реализации методики анализа, поправки на значение Θдоб (Θразб) (аналогично 6.3.3).
Если данный критерий не выполняется хотя бы для одного из Θдоб (Θразб), принимают решение о доработке методики.
10.3.4 При незначимости Θдоб (Θразб) или при принятом для методики анализа решении о введении в результаты анализа поправки показатель правильности методики анализа [верхнюю (Dс.в), нижнюю (Dс.н) границы, в которых неисключенная систематическая составляющая погрешности находится с принятой вероятностью Р = 0,95] рассчитывают по формуле
Dс.в = |Dс.н| = Dc
= 1,96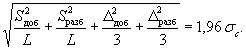 (70)
(70)
Примечание - В случае невозможности организации эксперимента в разных лабораториях экспериментальные данные получают в одной лаборатории в условиях внутрилабораторной прецизионности (серии результатов единичного анализа получают в разное время, разные операторы, используя разные партии реактивов одного типа, разные наборы мерной посуды и т.п.). Результаты единичного анализа внутри каждой серии получают в условиях повторяемости. В этом случае показатель правильности методики анализа (границы, в которых неисключенная систематическая погрешность методики анализа находится с принятой вероятностью Р = 0,95) рассчитывают по формуле
Dс.в = |Dс.н| = Dc
= 1,96 ![]() (71)
(71)
где Sл.доб, Sл.разб - выборочные СКО результатов анализа пробы и пробы с добавкой, рассчитанные в соответствии с 10.3.2 на основе результатов, полученных в условиях внутрилабораторной прецизионности;
k - коэффициент, учитывающий условия проведения эксперимента. k может принимать значения от 1,2 до 2,0.
10.4 Оценка показателя точности методики анализа
10.4.1 Верхнюю (Dв) и нижнюю (Dн) границы, в которых погрешность результата анализа1) находится с принятой вероятностью Р = 0,95, рассчитывают по формуле
Dв = |Dн|
= D
= 1,96![]() (72)
(72)
1) При незначимости Θдоб (Θразб) или при принятии решения о введении поправки в результат анализа.
Примечание - В случае, если учет Θдоб (Θразб) при вычислении показателя правильности методики анализа
Dс.в(н) = (Θдоб + Θразб) ± 1,96 sс, (73)
где Dс.в(н) - верхняя и нижняя границы, в которых систематическая погрешность методики анализа находится с принятой вероятностью Р = 0,95, не приводит к превышению характеристики погрешности результатов анализа над допускаемой, поправку в результат на значение Θдоб (Θразб) можно не вносить.
В этом случае показатель точности методики анализа рассчитывают по формуле
Dв(н) = (Θдоб + Θразб) ± 1,96s(D), (74)
10.4.2 При необходимости по найденным для каждого из поддиапазонов измерений значениям D устанавливают функциональную зависимость D от содержания определяемого компонента для всего диапазона измерений с учетом рекомендаций 6.5.
11 Метод оценки показателей качества методики анализа с применением набора образцов для оценивания в виде однородных и стабильных по составу рабочих проб
11.1 Основные допущения
11.1.1 Распределение случайной погрешности результата анализа принимают нормальным.
11.1.3 Приписанная характеристика погрешности результата анализа формируется в соответствии с моделью, приведенной в 5.2.
Примечание - Математическое ожидание измеряемой характеристики, полученное на основе результатов данного межлабораторного эксперимента, может быть использовано в качестве опорного значения ОО [3.22, перечисление г)] при контроле показателей качества методики при ее реализации в лабораториях.
11.1.4 Показатель точности методики анализа устанавливают на основе показателя воспроизводимости.
11.2 Оценка показателей прецизионности (повторяемости и воспроизводимости) методики анализа
11.2.1 Оценка показателей повторяемости и воспроизводимости методики анализа может быть проведена с использованием ОО (по 11.1.2). Общие требования к организации эксперимента и методы оценки аналогичны рассмотренным в 6.1 - 6.2.
11.2.2 Устанавливают зависимость sR от содержания определяемого компонента с учетом 6.5.2. При необходимости диапазон измерений разбивают на поддиапазоны, в пределах которых можно принять постоянство sR.
11.3 Оценка показателя точности методики анализа
Верхнюю (Dв) и нижнюю (Dн) границы, в которых погрешность результата анализа находится с принятой вероятностью Р = 0,95, рассчитывают по формуле
Dв = |Dн| = D = 1,96sR. (75)
Примечания
1 Этот метод оценки используют, когда применение методов, приведенных в разделах 6 - 10, 12, не представляется возможным.
2 При применении данного метода оценки показателя точности методики анализа целесообразно говорить об единообразии измерений, а не об их единстве.
12 Метод оценки показателей качества методики анализа с применением расчетного способа1)
1) Данный метод допускается применять при невозможности организации межлабораторного эксперимента и отсутствии принятого опорного значения по 3.22, т.е. при невозможности применения методов оценки показателей точности, правильности, прецизионности, изложенных в разделах 6 - 11.
12.1 Основные допущения
12.1.1 Распределение случайной погрешности результата анализа принимают нормальным.
12.1.2 Распределение составляющих систематической погрешности принимают равномерным.
12.1.3 Приписанная характеристика случайной погрешности представляет собой СКО результатов единичного анализа, полученных в условиях повторяемости.
12.1.4 Приписанную характеристику систематической погрешности методики анализа рассчитывают как сумму составляющих систематической погрешности.
12.1.5 При расчетном способе к факторам, которые формируют систематическую погрешность методики анализа, могут быть отнесены все факторы, перечисленные в 4.8, за исключением случайных эффектов, количественную оценку влияния которых учитывают при расчете СКО результатов единичного анализа, полученных в условиях повторяемости.
Примечания
1 Расчетный способ может быть применен для методик анализа, для которых возможно выявить и оценить влияние факторов, формирующих систематическую погрешность методики анализа. При этом необязательно количественно оценивать каждую составляющую погрешности, так как при определенных обстоятельствах возможна оценка суммарного влияния нескольких факторов.
2 Экспериментальная оценка значений влияния отдельных факторов, формирующих систематическую погрешность, может быть проведена с использованием методов, указанных в разделах 6 - 10.
12.2 Оценка показателя повторяемости методики анализа
12.2.1 Оценка показателя повторяемости методики анализа может быть проведена с использованием рабочих проб2). Общие требования к организации эксперимента и методы оценки аналогичны рассмотренным в 6.1.
2) При этом используемые пробы однородны и стабильны во время проведения эксперимента (см. [1]).
12.2.2 Планирование эксперимента по оценке показателя повторяемости осуществляют в соответствии с 6.1.14. Оценку показателя повторяемости методики анализа проводят в соответствии с 6.2.1.
12.3 Оценка показателя правильности методики анализа
12.3.1 Выявляют факторы, формирующие систематическую погрешность. Систематическая погрешность может быть обусловлена погрешностями:
- приготовления растворов (взятие навески, ее растворение, разбавление растворов, концентрирование и т.п.);
- приготовления образцов для градуировки;
- используемых при анализе средств измерений, в том числе СО или АС;
- построения градуировочного графика;
- используемого метода анализа;
- неполнотой выделения определяемого компонента;
- наличием влияющих факторов пробы и т.п.
12.3.2 Расчетным или экспериментальным путем оценивают характеристику каждой составляющей систематической погрешности.
12.3.3 Показатель правильности методики анализа (границы неисключенной систематической погрешности Dс.в = |Dс.н| = Dc) вычисляют путем построения композиции неисключенных систематических погрешностей средств измерений, метода и погрешностей, вызванных другими источниками. При равномерном распределении неисключенных систематических погрешностей эти границы (без учета знака) можно вычислить по формуле
![]() (76)
(76)
где Θi - граница i-й неисключенной составляющей систематической погрешности;
K - коэффициент, определяемый принятой доверительной вероятностью. Коэффициент K принимают равным 1,1 при доверительной вероятности Р = 0,95.
Примечание - Примером оценивания показателя правильности расчетным способом может служить алгоритм, приведенный в ГОСТ 12.1.016.
12.4 Оценка показателя точности методики анализа
12.4.1 Верхнюю (Dв) и нижнюю (Dн) границы, в которых погрешность результата анализа находится с принятой вероятностью Р = 0,95, рассчитывают по формуле
 (77)
(77)
Примечание - Рассчитанное значение показателя точности методики по сути является эквивалентом расширенной неопределенности результатов анализа.
12.4.2 При необходимости по найденным для каждого из поддиапазонов измерений значениям D устанавливают функциональную зависимость D от содержания определяемого компонента для всего диапазона измерений с учетом рекомендаций 6.5.
Приложение
А
(обязательное)
Условные обозначения, используемые в настоящих рекомендациях
L - число лабораторий, принимающих участие в эксперименте.
l - номер лаборатории.
N - число результатов единичного анализа (параллельных определений), полученных в одной лаборатории при проведении эксперимента.
n - число параллельных определений, предусмотренное прописью методики анализа.
i - номер результата единичного анализа (параллельного определения).
М - число образцов для оценивания.
m - номер образца для оценивания.
J - число влияющих факторов пробы.
j - номер влияющего фактора пробы.
Хтli - результат параллельного определения (единичного анализа).
Xml - среднее арифметическое результатов параллельных определений (результатов единичного анализа), полученных в лаборатории.
Хт - среднее арифметическое результатов анализа (результатов единичного анализа), полученных в разных лабораториях.
S![]() - выборочная дисперсия результатов единичного
анализа, полученных в l-й лаборатории.
- выборочная дисперсия результатов единичного
анализа, полученных в l-й лаборатории.
Srm - выборочное СКО, характеризующее повторяемость результатов единичного анализа.
S![]() - выборочная дисперсия, характеризующая повторяемость
результатов единичного анализа.
- выборочная дисперсия, характеризующая повторяемость
результатов единичного анализа.
srm(sr) - показатель повторяемости методики анализа в виде СКО.
rnm(rn) - показатель повторяемости методики анализа в виде предела повторяемости для п параллельных определений.
S![]() - выборочная
дисперсия, характеризующая разброс средних арифметических результатов
единичного анализа.
- выборочная
дисперсия, характеризующая разброс средних арифметических результатов
единичного анализа.
S![]() - выборочная дисперсия, характеризующая разброс
средних арифметических результатов единичного анализа, полученных в
условиях внутрилабораторной прецизионности.
- выборочная дисперсия, характеризующая разброс
средних арифметических результатов единичного анализа, полученных в
условиях внутрилабораторной прецизионности.
Sл - выборочное СКО результатов анализа, полученных в условиях внутрилабораторной прецизионности.
SRm - выборочное СКО результатов анализа, полученных в условиях воспроизводимости.
S![]() - выборочное СКО результатов анализа, полученных в
условиях внутрилабораторной прецизионности.
- выборочное СКО результатов анализа, полученных в
условиях внутрилабораторной прецизионности.
sRm(sR) - показатель воспроизводимости методики анализа в виде СКО результатов анализа.
Rm - показатель воспроизводимости методики анализа в виде предела воспроизводимости для двух результатов анализа.
Ст - аттестованное значение образца для оценивания.
С, Сввед - значение введенной добавки.
Do - погрешность аттестованного значения OO.
Θт(Θ) - оценка систематической погрешности методики анализа.
Dс.в = |Dс.н| = Dс
(Dс.в т = |Dс.н т| = Dс т) - верхняя и нижняя границы, в которых находится неисключенная систематическая погрешность методики анализа с принятой вероятностью Р.
sс т(sс) - СКО систематической погрешности методики анализа.
s(D) (s(Dm)) - СКО погрешности методики анализа.
Dв = |Dн| = D
(Dв т = Dн m = Dm) - верхняя и нижняя границы, в которых находится погрешность результата анализа с принятой вероятностью Р.
xн jl - результат анализа пробы с содержанием влияющего фактора вблизи его нижней границы.
![]() н j -
среднее арифметическое
результатов анализа пробы с содержанием j-го влияющего фактора
вблизи его нижней границы.
н j -
среднее арифметическое
результатов анализа пробы с содержанием j-го влияющего фактора
вблизи его нижней границы.
xв jl - результат анализа пробы с содержанием влияющего фактора вблизи его верхней границы.
![]() в j -
среднее арифметическое
результатов анализа пробы с содержанием j-го влияющего фактора
вблизи его верхней границы.
в j -
среднее арифметическое
результатов анализа пробы с содержанием j-го влияющего фактора
вблизи его верхней границы.
t (tдоб, tразб) - расчетное значение критерия Стьюдента (t-критерия).
tтабл - табличное значение критерия Стьюдента (t-критерия).
Gт (max) - расчетное значение критерия Кохрена.
Gтабл - табличное значение критерия Кохрена.
v, f - число степеней свободы.
DLc - лабораторная составляющая систематической погрешности, формирующая межлабораторную вариацию.
Dл - характеристика погрешности любого из совокупности результатов анализа, полученных в лаборатории.
a1, a2 (λ1, λ2) - коэффициенты зависимости показателя точности (воспроизводимости) от измеряемого содержания.
Θв j, Θн j - границы, в которых находится составляющая систематической погрешности, обусловленная влиянием j-го фактора пробы.
Θj - эффект влияния j-го фактора пробы.
Θв - варьируемая часть систематической погрешности.
Θoв = |Θoн| = Θo - постоянная часть систематической погрешности.
ξ - коэффициент, используемый при введении ограничений на значение поправки.
xсl - результаты анализа, полученные по методике сравнения.
Dм - характеристика погрешности результатов анализа, полученных по методике сравнения.
Sc - СКО, характеризующее разброс результатов анализа, полученных по исследуемой методике и по методике сравнения.
![]() -
СКО, характеризующее разброс результатов анализа, полученных по исследуемой
методике и по методике сравнения в условиях внутрилабораторной прецизионности.
-
СКО, характеризующее разброс результатов анализа, полученных по исследуемой
методике и по методике сравнения в условиях внутрилабораторной прецизионности.
хl, х’рl, х"l, x’l - результаты анализа пробы, разбавленной пробы и разбавленной пробы с добавкой, пробы с добавкой.
![]() ,
, ![]() ’ -
средние арифметические результатов анализа пробы и пробы с
добавкой.
’ -
средние арифметические результатов анализа пробы и пробы с
добавкой.
S1, S2 - СКО, характеризующие разброс результатов анализа пробы без добавки и пробы с добавкой.
S1л, S2л - СКО, характеризующие разброс результатов анализа пробы без добавки и пробы с добавкой, полученные в условиях внутрилабораторной прецизионности.
Θlдоб, Θlразб - разности «введено - найдено» и разности между результатами анализа пробы без добавки и пробы с добавкой.
![]() доб,
доб, ![]() разб -
средние арифметические разностей Θlдоб,
Θlразб.
разб -
средние арифметические разностей Θlдоб,
Θlразб.
Sдоб, Sразб - СКО разностей Θlдоб, Θlразб.
Sл.доб, Sл.разб - СКО разностей Θlдоб, Θlразб результатов, полученных в условиях внутрилабораторной прецизионности.
Dдо6 - погрешность аттестованного значения добавки.
Dразб - погрешность, обусловленная процедурой разбавления пробы.
Θi - границы i-й неисключенной составляющей систематической погрешности.
К - коэффициент, определяемый принятой доверительной вероятностью.
g - отношение показателей воспроизводимости и повторяемости.
k - коэффициент, учитывающий условия проведения эксперимента.
Dc*
(![]() c*) - систематическая
погрешность методики анализа (оценка систематической погрешности методики
анализа).
c*) - систематическая
погрешность методики анализа (оценка систематической погрешности методики
анализа).
D*Lc (![]() *Lc) - лабораторная
составляющая систематической погрешности (оценка лабораторной составляющей
систематической погрешности).
*Lc) - лабораторная
составляющая систематической погрешности (оценка лабораторной составляющей
систематической погрешности).
![]() -
случайная погрешность результатов единичного анализа, полученных в условиях
повторяемости (оценка случайной погрешности результатов анализа, полученных в
условиях повторяемости).
-
случайная погрешность результатов единичного анализа, полученных в условиях
повторяемости (оценка случайной погрешности результатов анализа, полученных в
условиях повторяемости).
![]() -
случайная погрешность результатов анализа, полученных в условиях
воспроизводимости (оценка случайной погрешности результатов анализа, полученных
в условиях воспроизводимости).
-
случайная погрешность результатов анализа, полученных в условиях
воспроизводимости (оценка случайной погрешности результатов анализа, полученных
в условиях воспроизводимости).
Приложение
Б
(рекомендуемое)
Сведения об оценке показателей точности, правильности, прецизионности
методики анализа
|
Номер образца т = 1, ..., M |
Число лабораторий L1) |
Число результатов единичного анализа N |
Принятое опорное значение Cm |
Среднее арифметическое значение результатов анализа Xm |
Оценка СКО повторяемости srm |
Оценка СКО воспроизводимости sRm |
Метод оценки показателя правильности |
Оценка показателя правильности ±Dc m |
Оценка показателя точности ±Dm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) В случае, если экспериментальные данные были получены в одной лаборатории в условиях внутрилабораторной прецизионности, в данной графе указывают число серий результатов единичного анализа.
Приложение
В
(справочное)
Составляющие погрешности результата анализа
Таблица В.1 - Обозначения и пояснения
|
Обозначение |
Наименование |
Пояснение |
|
D |
Систематическая погрешность методики анализа |
Разность между математическим ожиданием результатов единичного анализа, полученных во всех лабораториях, применяющих данную методику анализа, и истинным (или в его отсутствие принятым опорным) значением. Примечание - На практике оперируют оценкой
где С - истинное [или в его отсутствие принятое опорное (по 3.22, перечисления а), б), в)] значение содержания компонента в пробе вещества (материала) |
|
D |
Лабораторная составляющая систематической погрешности |
Разность между математическим ожиданием результатов единичного анализа, полученных в отдельной лаборатории при реализации методики анализа, и математическим ожиданием результатов единичного анализа, полученных в условиях воспроизводимости. Примечание - На практике оперируют оценкой
где
|
|
|
Случайная погрешность результатов единичного анализа, полученных в условиях повторяемости |
Разность между результатом единичного анализа и математическим ожиданием результатов единичного анализа, полученных в условиях повторяемости. Примечание - На практике оперируют оценкой
где X - результат единичного анализа;
|
|
|
Случайная погрешность результатов анализа, полученных в условиях воспроизводимости |
где DLc - лабораторная составляющая систематической погрешности, формирующая межлабораторную вариацию;
Примечание - |
Приложение
Г
(справочное)
Общие требования к постановке эксперимента по оценке показателей
качества методики анализа
Эксперимент по оценке показателей качества методики анализа планирует совет экспертов, в состав которого входят специалисты (аналитики и метрологи), имеющие достаточный опыт разработки и аттестации методик анализа.
Эти специалисты должны знать:
- формы представления и способы выражения характеристик и норм погрешности результатов анализа и их связь с показателями качества методик анализа;
- формы представления результатов анализа;
- номенклатуру характеристик погрешности и формы их представления для всех возможных случаев применения;
- расчетные и экспериментально-расчетные методы оценки показателей качества методик анализа;
- основные методы измерений, положенные в основу методик анализа;
- методологию планирования и проведения метрологических исследований при разработке методики анализа.
Основными этапами планирования эксперимента являются:
- составление структурной схемы методики анализа и выявление возможных источников погрешности;
- анализ состава исходных проб веществ и материалов, изучение возможного влияния матриц проб на результаты анализа;
- уточнение диапазона и области применения методики анализа на основе проведенного анализа состава исходных проб;
- определение числа точек диапазона, для которых будет проведена оценка показателей качества методики анализа;
- определение наличия стандартных образцов, адекватных по составу анализируемым пробам, методики сравнения, возможности внесения добавки в анализируемую пробу и т.д.;
- выбор метода оценки показателей качества методики анализа;
- определение числа лабораторий, которые должны быть вовлечены в совместный оценочный эксперимент;
- назначение числа параллельных определений, которое должно быть получено каждой лабораторией;
- определение сроков проведения оценочного эксперимента.
Документ (проект документа) на методику анализа должен содержать подробное и четкое описание всех деталей подготовки, проведения анализа, вычисления результата анализа, требования к числу результатов параллельных определений, а также требования к условиям проведения анализа, оборудованию, средствам измерений, реактивам и материалам.
Лаборатории, участвующие в эксперименте по оценке показателей качества методики анализа, должны быть выбраны случайным образом из числа лабораторий, применяющих данную методику анализа. Если к эксперименту привлекают лабораторию, не применяющую данную методику анализа, то этой лаборатории необходимо заранее освоить процедуру выполнения анализа в соответствии с методикой анализа. При выборе лабораторий необходимо учитывать возможность привлечения лабораторий, находящихся в разных регионах страны или в различных климатических зонах. Лаборатории должны иметь необходимые средства измерений, оборудование, реактивы и материалы. Применяемые средства измерений должны быть подвергнуты поверке (калибровке). Стандартные образцы должны соответствовать ГОСТ 8.315, аттестованные смеси - РМГ 60. При этом как при получении текущих результатов анализа, так и при получении результатов в ходе оценочного эксперимента в лаборатории должны быть внедрены меры для обеспечения и контроля качества, гарантирующие стабильность и подконтрольность процесса получения результатов анализа. Такие меры включают в себя, например, наличие персонала соответствующей квалификации, правильную эксплуатацию и поверку (калибровку) средств измерений, применение документированных методик анализа, эталонов, стандартных образцов, реактивов требуемого качества.
В каждой лаборатории должен быть назначен ответственный за организацию фактического выполнения эксперимента. Результаты анализа, полученные в ходе оценочного эксперимента, должны содержать, по меньшей мере, на одну значащую цифру больше числа значащих цифр, установленного в методике анализа для результата анализа.
Выбор числа лабораторий, принимающих участие в межлабораторном эксперименте, осуществляют в соответствии с таблицами Г.1 и Г.2, а также в соответствии с [1], [4].
Таблица Г.1 - Значения неопределенности оценки СКО воспроизводимости
|
Число результатов единичного анализа N |
||||||||||||||||
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
|
|
g = 1,2 |
|||||||||||||||
|
5 |
0,50 |
0,42 |
0,38 |
0,35 |
0,33 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
8 |
0,38 |
0,32 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
10 |
0,34 |
0,29 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
g = 1,4 |
|||||||||||||||
|
5 |
0,54 |
0,48 |
0,45 |
0,43 |
0,42 |
0,41 |
0,40 |
0,39 |
0,39 |
0,38 |
0,38 |
0,38 |
0,37 |
0,37 |
0,37 |
0,37 |
|
8 |
0,36 |
0,37 |
0,34 |
0,33 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
10 |
0,36 |
0,32 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
g = 1,6 |
|||||||||||||||
|
5 |
0,57 |
0,53 |
0,50 |
0,49 |
0,48 |
0,47 |
0,46 |
0,46 |
0,46 |
0,45 |
0,45 |
0,45 |
0,45 |
0,44 |
0,44 |
0,44 |
|
8 |
0,43 |
0,40 |
0,38 |
0,37 |
0,36 |
0,35 |
0,35 |
0,35 |
0,34 |
0,34 |
0,34 |
0,34 |
0,34 |
0,34 |
0,34 |
0,33 |
|
10 |
0,38 |
0,35 |
0,33 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
g = 1,8 |
|||||||||||||||
|
5 |
- |
0,56 |
0,54 |
0,53 |
0,52 |
0,51 |
0,51 |
0,51 |
0,50 |
0,50 |
0,50 |
0,50 |
0,50 |
0,50 |
0,49 |
0,49 |
|
8 |
0,45 |
0,42 |
0,41 |
0,40 |
0,39 |
0,39 |
0,39 |
0,38 |
0,38 |
0,38 |
0,38 |
0,38 |
0,38 |
0,37 |
0,37 |
0,37 |
|
10 |
0,40 |
0,37 |
0,36 |
0,35 |
0,35 |
0,34 |
0,34 |
0,34 |
0,34 |
0,33 |
0,33 |
0,33 |
0,33 |
0,33 |
0,33 |
0,33 |
|
|
g = 2,0 |
|||||||||||||||
|
5 |
- |
0,58 |
0,57 |
0,56 |
0,55 |
0,55 |
0,54 |
0,54 |
0,54 |
0,54 |
0,54 |
0,53 |
0,53 |
0,53 |
0,53 |
0,53 |
|
8 |
0,46 |
0,44 |
0,43 |
0,42 |
0,42 |
0,41 |
0,41 |
0,41 |
0,41 |
0,41 |
0,41 |
0,40 |
0,40 |
0,40 |
0,40 |
0,40 |
|
10 |
0,41 |
0,39 |
0,38 |
0,37 |
0,37 |
0,37 |
0,36 |
0,36 |
0,36 |
0,36 |
0,36 |
0,36 |
0,36 |
0,36 |
0,35 |
0,35 |
|
15 |
0,33 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
Таблица Г.2 - Значения неопределенности оценок систематической погрешности методики анализа
|
Число результатов единичного анализа N |
||||||||||||||||
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
|
|
g = 1,2 |
|||||||||||||||
|
4 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,58 |
0,58 |
0,58 |
0,58 |
|
5 |
- |
- |
- |
0,58 |
0,57 |
0,56 |
0,55 |
0,54 |
0,54 |
0,53 |
0,53 |
0,53 |
0,52 |
0,52 |
0,52 |
0,52 |
|
8 |
0,56 |
0,51 |
0,48 |
0,46 |
0,45 |
0,44 |
0,43 |
0,43 |
0,42 |
0,42 |
0,42 |
0,42 |
0,41 |
0,41 |
0,41 |
0,41 |
|
10 |
0,50 |
0,45 |
0,43 |
0,41 |
0,40 |
0,39 |
0,39 |
0,38 |
0,38 |
0,38 |
0,37 |
0,37 |
0,37 |
0,37 |
0,37 |
0,36 |
|
15 |
0,41 |
0,37 |
0,35 |
0,34 |
0,33 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
20 |
0,35 |
0,32 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
g = 1,4 |
|||||||||||||||
|
8 |
- |
0,56 |
0,54 |
0,53 |
0,53 |
0,52 |
0,52 |
0,51 |
0,51 |
0,51 |
0,51 |
0,50 |
0,50 |
0,50 |
0,50 |
0,50 |
|
10 |
0,53 |
0,50 |
0,49 |
0,48 |
0,47 |
0,46 |
0,46 |
0,46 |
0,46 |
0,45 |
0,45 |
0,45 |
0,45 |
0,45 |
0,45 |
0,45 |
|
15 |
0,44 |
0,41 |
0,40 |
0,39 |
0,38 |
0,38 |
0,38 |
0,37 |
0,37 |
0,37 |
0,37 |
0,37 |
0,37 |
0,37 |
0,37 |
0,36 |
|
20 |
0,38 |
0,36 |
0,34 |
0,34 |
0,33 |
0,33 |
0,33 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
g = 1,6 |
|||||||||||||||
|
8 |
- |
- |
0,58 |
0,57 |
0,57 |
0,57 |
0,56 |
0,56 |
0,56 |
0,56 |
0,56 |
0,55 |
0,55 |
0,55 |
0,55 |
0,55 |
|
10 |
0,56 |
0,53 |
0,52 |
0,51 |
0,51 |
0,51 |
0,50 |
0,50 |
0,50 |
0,50 |
0,50 |
0,50 |
0,49 |
0,49 |
0,49 |
0,49 |
|
15 |
0,45 |
0,44 |
0,43 |
0,42 |
0,42 |
0,41 |
0,41 |
0,41 |
0,41 |
0,41 |
0,41 |
0,40 |
0,40 |
0,40 |
0,40 |
0,40 |
|
20 |
0,39 |
0,38 |
0,37 |
0,36 |
0,36 |
0,36 |
0,36 |
0,35 |
0,35 |
0,35 |
0,35 |
0,35 |
0,35 |
0,35 |
0,35 |
0,35 |
|
25 |
0,35 |
0,34 |
0,33 |
0,33 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
g = 1,8 |
|||||||||||||||
|
8 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,58 |
0,58 |
0,58 |
|
10 |
0,57 |
0,55 |
0,54 |
0,54 |
0,53 |
0,53 |
0,53 |
0,53 |
0,53 |
0,53 |
0,52 |
0,52 |
0,52 |
0,52 |
0,52 |
0,52 |
|
15 |
0,47 |
0,45 |
0,44 |
0,44 |
0,44 |
0,43 |
0,43 |
0,43 |
0,43 |
0,43 |
0,43 |
0,43 |
0,43 |
0,43 |
0,43 |
0,43 |
|
20 |
0,40 |
0,39 |
0,38 |
0,38 |
0,38 |
0,38 |
0,37 |
0,37 |
0,37 |
0,37 |
0,37 |
0,37 |
0,37 |
0,37 |
0,37 |
0,37 |
|
25 |
0,36 |
0,35 |
0,34 |
0,34 |
0,34 |
0,34 |
0,33 |
0,33 |
0,33 |
0,33 |
0,33 |
0,33 |
0,33 |
0,33 |
0,33 |
0,33 |
|
30 |
0,33 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
g = 2,0 |
|||||||||||||||
|
10 |
0,58 |
0,57 |
0,56 |
0,55 |
0,55 |
0,55 |
0,55 |
0,55 |
0,55 |
0,54 |
0,54 |
0,54 |
0,54 |
0,54 |
0,54 |
0,54 |
|
15 |
0,47 |
0,46 |
0,46 |
0,45 |
0,45 |
0,45 |
0,45 |
0,45 |
0,45 |
0,44 |
0,44 |
0,44 |
0,44 |
0,44 |
0,44 |
0,44 |
|
20 |
0,41 |
0,40 |
0,40 |
0,39 |
0,39 |
0,39 |
0,39 |
0,39 |
0,39 |
0,39 |
0,38 |
0,38 |
0,38 |
0,38 |
0,38 |
0,38 |
|
25 |
0,37 |
0,36 |
0,35 |
0,35 |
0,35 |
0,35 |
0,35 |
0,35 |
0,35 |
0,34 |
0,34 |
0,34 |
0,34 |
0,34 |
0,34 |
0,34 |
|
30 |
0,33 |
0,33 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
Примечания к таблицам Г.1 и Г.2
1 ![]()
2 При других значениях g и числа лабораторий L - см. [1], [4].
3 Число лабораторий, меньшее числа, указанного в таблицах, приводит к худшим значениям неопределенности оценок СКО воспроизводимости и систематической погрешности.
4 Число лабораторий, превышающее число, указанное в таблицах, приводит к лучшим значениям неопределенности оценок СКО воспроизводимости и систематической погрешности.
Приложение
Д
(справочное)
Форма представления результатов единичного анализа образцов для
оценивания
|
Информационные данные ________________________________________________________________ наименование организации (предприятия) ________________________________________________________________ наименование лаборатории ________________________________________________________________ адрес, телефон руководитель организации (предприятия) ________________________________________________________________ руководитель лаборатории Сведения об аттестатах аккредитации лаборатории (номер, дата выдачи, кем выданы, срок действия) _____________________________________________________________ Наименование методики анализа ______________________________________________ Сведения о поверке (калибровке) средств измерений, используемых в методике анализа (дата и номер свидетельства о поверке, место поверки, наименование организации, осуществившей поверку) _________________________________________ Сведения об аттестации вспомогательного оборудования ________________________ Дата начала эксперимента ___________________________________________________ Дата окончания эксперимента ________________________________________________ Квалификация оператора, выполнившего анализы OO __________________________ Таблица - Результаты анализа образцов для оценивания
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Приложение
Е
(справочное)
Статистические таблицы
Таблица Е.1 - Критерий Кохрена. Критические значения (Gтабл) для доверительной вероятности Р = 0,95
|
v = N - 1 |
|||||
|
1 |
2 |
3 |
4 |
5 |
|
|
2 |
0,999 |
0,975 |
0,939 |
0,906 |
0,877 |
|
3 |
0,967 |
0.871 |
0,798 |
0,746 |
0,707 |
|
4 |
0,906 |
0,768 |
0,684 |
0,629 |
0,590 |
|
5 |
0,841 |
0,684 |
0,598 |
0,544 |
0,506 |
|
6 |
0,781 |
0,616 |
0,532 |
0,480 |
0,445 |
|
7 |
0,727 |
0,561 |
0,480 |
0,431 |
0,397 |
|
8 |
0,680 |
0,516 |
0,438 |
0,391 |
0,360 |
|
9 |
0,638 |
0,478 |
0,403 |
0,358 |
0,329 |
|
10 |
0,602 |
0,445 |
0,373 |
0,331 |
0,303 |
|
11 |
0,570 |
0,417 |
0,348 |
0,308 |
0,281 |
|
12 |
0,541 |
0,392 |
0,326 |
0,288 |
0,262 |
|
13 |
0,515 |
0,371 |
0,307 |
0,271 |
0,243 |
|
14 |
0,492 |
0,352 |
0,291 |
0,255 |
0,232 |
|
15 |
0,471 |
0,335 |
0,276 |
0,242 |
0,220 |
|
16 |
0,452 |
0,319 |
0,262 |
0,230 |
0,208 |
|
17 |
0,434 |
0,305 |
0,250 |
0,219 |
0,198 |
|
18 |
0,418 |
0,293 |
0,240 |
0,209 |
0,189 |
|
19 |
0,403 |
0,281 |
0,230 |
0,200 |
0,181 |
|
20 |
0,389 |
0,270 |
0,220 |
0,192 |
0,174 |
|
21 |
0,377 |
0,261 |
0,212 |
0,185 |
0,167 |
|
22 |
0,365 |
0,252 |
0,204 |
0,178 |
0,160 |
|
23 |
0,354 |
0,243 |
0,197 |
0,172 |
0,155 |
|
24 |
0,343 |
0,235 |
0,191 |
0,166 |
0,149 |
|
25 |
0,334 |
0,228 |
0,185 |
0,160 |
0,144 |
|
26 |
0,325 |
0,221 |
0,179 |
0,155 |
0,140 |
|
27 |
0,316 |
0,215 |
0,173 |
0,150 |
0,135 |
|
28 |
0,308 |
0,209 |
0,168 |
0,146 |
0,131 |
|
29 |
0,300 |
0,203 |
0,164 |
0,142 |
0,127 |
|
30 |
0,293 |
0,198 |
0,159 |
0,138 |
0,124 |
|
31 |
0,286 |
0,193 |
0,155 |
0,134 |
0,120 |
|
32 |
0,280 |
0,188 |
0,151 |
0,131 |
0,117 |
|
33 |
0,273 |
0,184 |
0,147 |
0,127 |
0,114 |
|
34 |
0,267 |
0,179 |
0,144 |
0,124 |
0,111 |
|
35 |
0,262 |
0,175 |
0,140 |
0,121 |
0,108 |
|
36 |
0,256 |
0,172 |
0,137 |
0,118 |
0,106 |
|
37 |
0,251 |
0,168 |
0,134 |
0,116 |
0.103 |
|
38 |
0,246 |
0,164 |
0,131 |
0,113 |
0,101 |
|
39 |
0,242 |
0,161 |
0,129 |
0,111 |
0,099 |
|
40 |
0,237 |
0,158 |
0,126 |
0,108 |
0,097 |
Таблица Е.2 - Процентные точки распределения Стьюдента Q = 2,5 % (двусторонний критерий)
|
t(f) |
f |
t(f) |
f |
t(f) |
f |
t(f) |
|
|
1 |
12,71 |
10 |
2.23 |
19 |
2.09 |
28 |
2,05 |
|
2 |
4,30 |
11 |
2,20 |
20 |
2,09 |
29 |
2,04 |
|
3 |
3.18 |
12 |
2,18 |
21 |
2,08 |
30 |
2,04 |
|
4 |
2,78 |
13 |
2,16 |
22 |
2,07 |
40 |
2,02 |
|
5 |
2,57 |
14 |
2,15 |
23 |
2,07 |
60 |
2,00 |
|
6 |
2,45 |
15 |
2,14 |
24 |
2,06 |
120 |
1,98 |
|
7 |
2,37 |
16 |
2,12 |
25 |
2,06 |
|
|
|
8 |
2,31 |
17 |
2,11 |
26 |
2,06 |
|
|
|
9 |
2,26 |
18 |
2,10 |
27 |
2,05 |
|
|
Таблица Е.3 - Процентные точки выборочного коэффициента корреляции (r*) Q = 2,5 % (двусторонний критерий) при числе степеней свободы f
|
r* |
f |
r* |
f |
r* |
|
|
1 |
0,997 |
11 |
0,553 |
25 |
0,381 |
|
2 |
0,950 |
12 |
0,532 |
30 |
0,349 |
|
3 |
0,878 |
13 |
0,514 |
35 |
0,325 |
|
4 |
0,811 |
14 |
0,497 |
40 |
0,304 |
|
5 |
0,754 |
15 |
0,482 |
45 |
0,287 |
|
6 |
0,707 |
16 |
0,468 |
50 |
0,273 |
|
7 |
0,666 |
17 |
0,456 |
60 |
0,250 |
|
8 |
0,632 |
18 |
0,444 |
|
|
|
9 |
0,602 |
19 |
0,433 |
|
|
|
10 |
0,576 |
20 |
0,423 |
|
|
Приложение
Ж
(справочное)
Виды зависимостей и формулы для расчета оценок коэффициентов этих
зависимостей
В качестве предполагаемых зависимостей характеристики случайной составляющей погрешности от анализируемого содержания рассматривают зависимости следующих видов:
I sR(C) = λ1 + λ2C;
II sR(C) = λ1 + λ2 lg C;
III lg [sR(C)] = λ1 + λ2 C;
IV lg [sR(C)] = λ1 + λ2l g C.
Коэффициенты перечисленных зависимостей оценивают методом наименьших квадратов.
Формулы для расчета оценок коэффициентов зависимостей вида:
I
![]()

II
![]()

III
![]()

IV
![]()
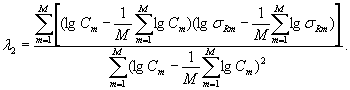
Адекватность экспериментальных данных выбранному виду зависимости проверяют путем сравнения выборочного коэффициента корреляции r*, вычисленного для зависимости соответствующего вида, с табличным значением rтабл (см. таблицу Е.3) при числе степеней свободы f = М - 2.
Значение выборочного коэффициента корреляции рассчитывают по формуле для зависимостей вида:
I
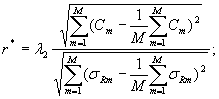
II

III

IV

Если r* > rтабл, то экспериментальные данные не противоречат предполагаемой зависимости. Если r* не превосходит rта6л, то экспериментальные данные противоречат зависимости выбранного вида. В этом случае рекомендуется выбрать другой вид зависимости из числа приведенных выше.
Если для всего диапазона измерений не удается установить один вид зависимости характеристики погрешности от измеряемого содержания, то целесообразно:
- либо разбить диапазон измерений на поддиапазоны, для каждого из которых установить свой вид зависимости;
- либо, если это приведет к превышению значения характеристики погрешности измерений над допускаемым значением, в качестве характеристики случайной составляющей погрешности в диапазоне измерений принять максимальное значение характеристики случайной составляющей погрешности результатов измерений содержаний компонентов проб веществ (материалов), выполняемых по методике, вычисленных для содержания определяемого компонента, соответствующего содержанию определяемого компонента в образцах для оценивания, т.е.
sR (С)
= const = max ![]() , m = 1, ..., M.
, m = 1, ..., M.
Приложение
И
(рекомендуемое)
Добавка к пробе (разбавленной пробе) и кратность разбавления в
зависимости от СКО воспроизводимости
|
СКО воспроизводимости, % содержания компонента в пробе |
Добавка, % содержания компонента в пробе, не менее |
Кратность разбавления пробы, не менее |
|
5 |
22 |
1,2 |
|
6 |
27 |
1,3 |
|
7 |
33 |
1,3 |
|
8 |
38 |
1,4 |
|
9 |
44 |
1,4 |
|
10 |
50 |
1,5 |
|
11 |
56 |
1,6 |
|
12 |
63 |
1,6 |
|
13 |
70 |
1,7 |
|
14 |
78 |
1,8 |
|
15 |
86 |
1,9 |
|
16 |
94 |
1,9 |
|
17 |
100 |
2,0 |
|
18 |
110 |
2,1 |
|
19 |
120 |
2,2 |
|
20 |
130 |
2,3 |
|
21 |
140 |
2,4 |
|
22 |
160 |
2,6 |
|
23 |
170 |
2,7 |
|
24 |
180 |
2,8 |
|
25 |
200 |
3,0 |
Библиография
|
Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения |
|
|
|
|
|
(ISO 5725-1-1994) |
(Accuracy (trueness and precision) of measurement methods and results. Part 1. General principles and definitions) |
|
Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений |
|
|
|
|
|
(ISO 5725-2-1994) |
(Accuracy (trueness and precision) of measurement methods and results. Part 2. Basic method for the determination of repeatability and reproducibility of a standard measurement method) |
|
[3] ИСО 5725-3-1994 |
Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений. |
|
|
|
|
(ISO 5725-3-1994) |
(Accuracy (trueness and precision) of measurement methods and results. Part 3. Intermediate measures of the precision of a standard measurement method) |
|
Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений. |
|
|
|
|
|
(ISO 5725-4-1994) |
(Accuracy (trueness and precision) of measurement methods and results. Part 4. Basic methods for the determination of the trueness of a standard measurement method) |
|
Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений. |
|
|
|
|
|
(ISO 5725-5-1998) |
(Accuracy (trueness and precision) of measurement methods and results. Part 5. Alternative methods for the determination of the precision of a standard measurement method) |
|
Русско-англо-немецко-испанский словарь основных и общих терминов в метрологии. - М.: ИПК Изд-во стандартов, 1998 |
|
|
[7] Руководство Еврохим/СИТАК (EURACHEM/CITAC Guide): |
Количественное описание неопределенности в аналитических измерениях. - 2-е изд., 2000. - Пер. с англ. - С.-Петербург: ВНИИМ им. Д.И. Менделеева, 2002 (Quantifying Uncertainty in Analytical Measurement (Second Edition) |
[8] H.B. Смирнов, И.В. Дунин-Барковский. Курс теории вероятностей и математической статистики для технических приложений. - М.: Наука, 1965
[9] В.В. Налимов. Применение математической статистики при анализе вещества. - М.: Физматгиз, 1960
Ключевые слова: количественный химический анализ, методика количественного химического анализа, результат единичного анализа, результат анализа, точность анализа, правильность анализа, прецизионность анализа, повторяемость анализа, воспроизводимость анализа, показатели качества методики анализа, приписанные характеристики погрешности анализа