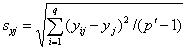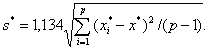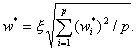ГОСТ Р ИСО 5725-5-2002
ГОСУДАРСТВЕННЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ТОЧНОСТЬ
(ПРАВИЛЬНОСТЬ И ПРЕЦИЗИОННОСТЬ)
МЕТОДОВ И РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Часть 5
Альтернативные
методы определения
прецизионности стандартного метода измерений
ГОССТАНДАРТ РОССИИ
Москва
Предисловие
1 РАЗРАБОТАН Федеральным государственным унитарным предприятием «Всероссийский научно-исследовательский институт метрологической службы» Госстандарта России (ВНИИМС), Всероссийским научно-исследовательским институтом стандартизации (ВНИИСтандарт), Всероссийским научно-исследовательским институтом классификации, терминологии и информации по стандартизации и качеству (ВНИИКИ) Госстандарта России
ВНЕСЕН Управлением метрологии и Научно-техническим управлением Госстандарта России
2 ПРИНЯТ И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Госстандарта России от 23 апреля 2002 г. № 161-ст
3 Настоящий стандарт представляет собой полный аутентичный текст международного стандарта ИСО 5725-5:1998 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений».
4 ВВЕДЕН ВПЕРВЫЕ
СОДЕРЖАНИЕ
ПРЕДИСЛОВИЕ К ГОСУДАРСТВЕННЫМ СТАНДАРТАМ РОССИЙСКОЙ ФЕДЕРАЦИИ ГОСТ Р ИСО 5725-1-2002 - ГОСТ Р ИСО 5725-6-2002 ПОД ОБЩИМ ЗАГОЛОВКОМ «ТОЧНОСТЬ (ПРАВИЛЬНОСТЬ И ПРЕЦИЗИОННОСТЬ) МЕТОДОВ И РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ»
Целью разработки Государственных стандартов Российской Федерации ГОСТ Р ИСО 5725-1- 2002, ГОСТ Р ИСО 5725-2-2002, ГОСТ Р ИСО 5725-3-2002, ГОСТ Р ИСО 5725-4-2002, ГОСТ Р ИСО 5725-5-2002, ГОСТ Р ИСО 5725-6-2002, далее - ГОСТ Р ИСО 5725, является прямое применение в Российской Федерации шести частей основополагающего международного стандарта ИСО 5725 под общим заголовком «Точность (правильность и прецизионность) методов и результатов измерений» в практической деятельности по метрологии (разработке, аттестации и применению методик выполнения измерений), стандартизации методов контроля (испытаний, измерений, анализа), испытаниям продукции, в том числе для целей подтверждения соответствия, оценке компетентности испытательных лабораторий согласно требованиям ГОСТ Р ИСО/МЭК 17025-2000.
ГОСТ Р ИСО 5725 представляют собой полный аутентичный текст шести частей международного стандарта ИСО 5725, в том числе:
ГОСТ Р ИСО 5725-1-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения»;
ГОСТ Р ИСО 5725-2-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений»;
ГОСТ Р ИСО 5725-3-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений»;
ГОСТ Р ИСО 5725-4-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений»;
ГОСТ Р ИСО 5725-5-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений»;
ГОСТ Р ИСО 5725-6-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике».
Каждая часть содержит аутентичный перевод предисловия и введения к международному стандарту ИСО 5725, а также предисловие к государственным стандартам Российской Федерации ГОСТ Р ИСО 5725-1-2002 - ГОСТ Р ИСО 5725-6-2002 и издается самостоятельно.
Пользование частями 2-6 ГОСТ Р ИСО 5725 в отдельности возможно только совместно с частью 1 (ГОСТ Р ИСО 5725-1), в которой установлены основные положения и определения, касающиеся всех частей ГОСТ Р ИСО 5725.
В соответствии с основными положениями ИСО 5725-1 (пункт 1.2) настоящий стандарт распространяется на методы измерений непрерывных (в смысле принимаемых значений в измеряемом диапазоне) величин, дающие в качестве результата измерений единственное значение. При этом это единственное значение может быть и результатом расчета, основанного на ряде измерений одной и той же величины.
Стандарты ИСО 5725 могут применяться для оценки точности выполнения измерений различных физических величин, характеризующих измеряемые свойства того или иного объекта, в соответствии со стандартизованной процедурой. При этом в пункте 1.2 стандарта ИСО 5725-1 особо отмечено, что стандарт может применяться для оценки точности выполнения измерений состава и свойств очень широкой номенклатуры материалов, включая жидкости, порошкообразные и твердые материалы - продукты материального производства или существующие в природе, при условии, что учитывают любую неоднородность материала.
Применяемый в международных стандартах термин «стандартный метод измерений» адекватен отечественному термину «стандартизованный метод измерений».
В ИСО 5725: 1994-1998 и ИСО/МЭК 17025-99 понятие «метод измерений» («measurement method») включает совокупность операций и правил, выполнение которых обеспечивает получение результатов с известной точностью. Таким образом, понятие «метод измерений» по ИСО 5725 и ИСО/МЭК 17025 адекватно понятию «методика выполнения измерений (МВИ)» по ГОСТ Р 8.563-96 «Государственная система обеспечения единства измерений. Методики выполнения измерений» (пункт 3.1) и соответственно значительно шире по смыслу, чем определение термина «метод измерений» в Рекомендации по межгосударственной стандартизации РМГ 29-99 «Государственная система обеспечения единства измерений. Метрология. Основные термины и определения» (пункт 7.2).
Более того, в оригинале ИСО 5725 очень часто употребляется в качестве понятия «метод измерений» и английский термин «test method», перевод которого на русский язык - «метод испытаний» (см. примечание 1 к пункту 3.2 ИСО 5725-1) и который по смыслу совпадает с термином 6.2 ИСО 5725-1 «standard measurement method» (стандартизованный метод измерений). Соответственно в качестве термина «результат измерений» в оригинале стандарта чаще используется английский термин «test result» (см. пункт 3.2 ИСО 5725-1), причем в контексте как с термином «test method» (см. пункт 3.2), так и с термином «measurement method» (см. в оригинале, например, пункты 1.2 или 7.2.1 ИСО 5725-1).
При этом следует иметь в виду, что область применения ИСО 5725 - точность стандартизованных методов измерений, в том числе предназначенных для целей испытаний продукции, позволяющих количественно оценить характеристики свойств (показателей качества и безопасности) объекта испытаний (продукции). Именно поэтому во всех частях стандарта результаты измерений характеристик образцов, взятых в качестве выборки из партии изделий (или проб, отобранных из партии материала), являются основой для получения результатов испытаний всей партии (объекта испытаний). Когда объектом испытаний является конкретный образец (test speciment, sample), результаты измерений и испытаний могут совпадать. Такой подход имеет место в примерах по определению показателей точности стандартного (стандартизованного) метода измерений, содержащихся в ИСО 5725.
Следует отметить, что в отечественной метрологии точность (accuracy) и погрешность (error) результатов измерений, как правило, определяются сравнением результата измерений с истинным или действительным (условно истинным) значением измеряемой физической величины (являющимися фактически эталонными значениями измеряемых величин, выраженными в узаконенных единицах).
В условиях отсутствия необходимых эталонов, обеспечивающих воспроизведение, хранение и передачу соответствующих значений единиц величин, необходимых для оценки погрешности (точности) результатов измерений, и в отечественной, и в международной практике за действительное значение зачастую принимают общее среднее значение (математическое ожидание) установленной (заданной) совокупности результатов измерений. В ИСО 5725 эта ситуация отражена в термине «принятое опорное значение» (см. пункты 3.5 и 3.6 ГОСТ Р ИСО 5725-1) и рекомендуется стандартом ГОСТ Р ИСО 5725-1 для использования в этих случаях и в отечественной практике.
Термины «правильность» (trueness) и «прецизионность» (precision) в отечественных нормативных документах по метрологии до настоящего времени не использовались. При этом «правильность» - степень близости результата измерений к истинному или условно истинному (действительному) значению измеряемой величины или в случае отсутствия эталона измеряемой величины - степень близости среднего значения, полученного на основании большой серии результатов измерений (или результатов испытаний), к принятому опорному значению. Показателем правильности обычно является значение систематической погрешности (см. пункт 3.7 ГОСТ Р ИСО 5725-1).
В свою очередь «прецизионность» - степень близости друг к другу независимых результатов измерений, полученных в конкретных установленных условиях. Эта характеристика зависит только от случайных факторов и не связана с истинным или условно истинным значением измеряемой величины (см. пункт 3.12 ГОСТ Р ИСО 5725-1). Мера прецизионности обычно вычисляется как стандартное (среднеквадратическое) отклонение результатов измерений, выполненных в определенных условиях. Количественные значения мер прецизионности существенно зависят от заданных условий. Экстремальные показатели прецизионности - повторяемость, сходимость (repeatability) и воспроизводимость (reproducibility) регламентируют и в отечественных нормативных документах, в том числе в большинстве государственных стандартов на методы контроля (испытаний, измерений, анализа) (см. пункты 3.12-3.20 ГОСТ Р ИСО 5725-1).
В соответствии с ИСО 5725 цель государственных стандартов ГОСТ Р ИСО 5725 состоит в том, чтобы:
а) изложить основные положения, которые следует иметь в виду при оценке точности (правильности и прецизионности) методов и результатов измерений при их применении, а также при планировании экспериментов по оценке различных показателей точности (ГОСТ Р ИСО 5725-1);
б) регламентировать основной способ экспериментальной оценки повторяемости (сходимости) и воспроизводимости методов и результатов измерений (ГОСТ Р ИСО 5725-2);
в) регламентировать процедуру получения промежуточных показателей прецизионности методов и результатов измерений, изложив условия их применения и методы оценки (ГОСТ Р ИСО 5725-3);
г) регламентировать основные способы определения правильности методов и результатов измерений (ГОСТ Р ИСО 5725-4);
д) регламентировать для применения в определенных обстоятельствах несколько альтернатив основным способам (ГОСТ Р ИСО 5725-2 и ГОСТ Р ИСО 5725-4) определения прецизионности и правильности методов и результатов измерений, приведенных в ГОСТ Р ИСО 5725-5;
е) изложить некоторые практические применения показателей правильности и прецизионности (ГОСТ Р ИСО 5725-6).
Представленные в виде таблицы рекомендации по применению основных положений ГОСТ Р ИСО 5725 в деятельности по метрологии, стандартизации, испытаниям, оценке компетентности испытательных лабораторий со ссылками на нормы государственных стандартов Российской Федерации, содержащих требования к выполнению соответствующих работ, приведены в приложении к предисловию в ГОСТ Р ИСО 5725-1.
Алгоритмы проведения экспериментов по оценке повторяемости, воспроизводимости, промежуточных показателей прецизионности, показателей правильности (характеристик систематической погрешности) методов и результатов измерений рекомендуется внедрять через программы экспериментальных метрологических исследований показателей точности (характеристик погрешности) результатов измерений, выполняемых по разрабатываемой МВИ, и (или) через программы контроля показателей точности применяемых МВИ.
Использование приведенных в приложениях А к каждому стандарту условных обозначений в качестве обязательных рекомендуется только для тех показателей точности, которые до настоящего времени в отечественной метрологической практике не использовались (например, для показателей по пунктам 3.9-3.12 ГОСТ Р ИСО 5725-1). Для остальных показателей и критериев используемые в ГОСТ Р ИСО 5725 условные обозначения, как правило, могут применяться наряду с условными обозначениями этих показателей и критериев, принятыми в действующих отечественных документах (например, предел повторяемости (сходимости) с условным обозначением r по пункту 3.16 ГОСТ Р ИСО 5725-1 наряду с условным обозначением d, принятым для этого показателя в ряде рекомендаций по метрологии, а также в государственных стандартах на методы испытаний продукции).
ПРЕДИСЛОВИЕ К МЕЖДУНАРОДНОМУ СТАНДАРТУ ИСО 5725
Международная организация по стандартизации (ИСО) является Всемирной федерацией национальных организаций по стандартизации (комитетов-членов ИСО). Разработка международных стандартов обычно осуществляется техническими комитетами ИСО. Каждый член ИСО, заинтересованный в деятельности соответствующего технического комитета, имеет право быть представленным в этом комитете. Правительственные и неправительственные международные организации, сотрудничающие с ИСО, также принимают участие в этой работе. ИСО тесно сотрудничает с Международной электротехнической комиссией (МЭК) по всем вопросам стандартизации в области электротехники.
Проекты международных стандартов, принятые техническими комитетами, направляются техническим комитетам-членам ИСО на голосование перед их утверждением Советом ИСО в качестве международных стандартов. Стандарты утверждаются в качестве международных в соответствии с установленными в ИСО требованиями: в случае их одобрения по меньшей мере 75 % комитетов-членов ИСО, принимавших участие в голосовании.
Международный стандарт ИСО 5725-5 был подготовлен Техническим комитетом ИСО/ТК 69 «Применение статистических методов», Подкомитетом ПК 6 «Методы и результаты измерений».
ИСО 5725 состоит из следующих частей под общим заголовком «Точность (правильность и прецизионность) методов и результатов измерений»:
Часть 1. Основные положения и определения
Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений
Часть 3. Промежуточные показатели прецизионности стандартного метода измерений
Часть 4. Основные методы определения правильности стандартного метода измерений
Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений
Часть 6. Использование значений точности на практике
ИСО 5725 (части 1-6) в совокупности аннулирует и заменяет ИСО 5725:1986, область распространения которого была расширена включением правильности (в дополнение к прецизионности) и условий промежуточной прецизионности (в дополнение к условиям повторяемости и воспроизводимости).
Приложение А является обязательным для настоящей части ИСО 5725, приложения В, С и D - справочные.
ВВЕДЕНИЕ К МЕЖДУНАРОДНОМУ СТАНДАРТУ ИСО 5725
0.1 В ИСО 5725 для описания точности метода измерений используют два термина: «правильность» и «прецизионность». Термин «правильность» характеризует степень близости среднего значения большого числа результатов испытаний к истинному или принятому опорному значению, термин «прецизионность» - степень близости результатов испытаний друг к другу.
0.2 Общие положения об этих понятиях представлены в ИСО 5725-1 и поэтому здесь не повторяются. Эта часть ИСО 5725 должна применяться совместно с ИСО 5725-1, поскольку в ней даны определения и общие положения.
0.3 ИСО 5725-2 посвящен методам количественной оценки прецизионности, а именно стандартных отклонений повторяемости и воспроизводимости посредством межлабораторных экспериментов. В нем рассматривается основной метод такой оценки, использующий эксперимент с однородными уровнями. ИСО 5725-5 описывает методы оценки, альтернативные этому основному.
a) При пользовании основным методом имеется риск, что оператор допустит, что результат измерения одной пробы повлияет на результат последующего измерения другой пробы того же материала, вызывая систематическую погрешность в оценке стандартных отклонений повторяемости и воспроизводимости. Когда этот риск считают значительным, модель с разделенными уровнями, описанная в ИСО 5725-5, может быть предпочтительнее, как снижающая этот риск.
b) Основной метод требует подготовки ряда идентичных проб материала для использования в эксперименте. С гетерогенными материалами это может быть невозможно, так как применение основного метода потом дает оценки стандартного отклонения воспроизводимости, которые искажаются различием между пробами. Схема для гетерогенного материала, приведенная в ИСО 5725-5, дает информацию о неоднородности проб, которая не выявляется основным методом; она может быть использована для расчетов оценки воспроизводимости, из которой исключена разница между пробами.
c) Основной метод требует проверок на наличие выбросов, чтобы идентифицировать данные, которые должны быть исключены из расчета стандартных отклонений повторяемости и воспроизводимости. Исключение выбросов может иногда значительно повлиять на оценку стандартных отклонений повторяемости и воспроизводимости; но на практике в случаях, когда применяют контроль выбросов, у аналитика есть основание принять решение, какие данные исключить. ИСО 5725-5 описывает робастные методы анализа данных, которые могут применяться для расчета стандартных отклонений повторяемости и воспроизводимости из данных, содержащих выбросы, без применения проверок на наличие выбросов в целях исключения таких данных, так что эти результаты больше не влияют на решение аналитика.
ГОСУДАРСТВЕННЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ТОЧНОСТЬ (ПРАВИЛЬНОСТЬ И ПРЕЦИЗИОННОСТЬ) МЕТОДОВ И РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Часть 5
Альтернативные методы определения прецизионности стандартного метода измерений
Accuracy (trueness and precision) of measurement methods and results.
Part 5. Alternative methods for the determination of the precision of a standard
measurement method
Дата введения 2002-11-01
1 Область применения
В настоящем стандарте детально представлены альтернативы основному методу определения стандартных отклонений повторяемости и воспроизводимости стандартного метода измерений, именуемые моделью эксперимента с разделенными уровнями и моделью эксперимента для гетерогенных материалов, а также описано использование робастных методов для анализа результатов экспериментов по оценке прецизионности без применения проверок наличия выбросов с целью их исключения из расчетов, и особенно - подробное использование одного из таких методов.
Настоящий стандарт дополняет ГОСТ Р ИСО 5725-2, описывая альтернативные методы, которые могут быть в отдельных случаях предпочтительнее основного метода, приведенного в ГОСТ Р ИСО 5725-2, и предусматривая робастный метод анализа, который дает оценки стандартных отклонений повторяемости и воспроизводимости, в меньшей мере зависимые от решений, принимаемых на основе данных аналитика, по сравнению с методами оценки, описанными в ГОСТ Р ИСО 5725-2.
2 Нормативные ссылки
В настоящем стандарте использованы ссылки на следующие стандарты:
ГОСТ Р ИСО 5725-1-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения.
ГОСТ Р ИСО 5725-2-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений
3 Определения
В настоящем стандарте применяют термины в соответствии с ИСО 3534-1 [1] и ГОСТ Р ИСО 5725-1.
Условные обозначения, использованные в ГОСТ Р ИСО 5725, приведены в приложении А.
4 Модель эксперимента с разделенными уровнями
4.1 Применение модели
4.1.1 Эксперимент с однородными уровнями, описанный в ГОСТ Р ИСО 5725-2, требует по две или более идентичных проб материала для испытаний в каждой лаборатории - участнице эксперимента на каждом уровне. При этом имеется риск, что оператор допустит влияние результата предыдущих измерений одной пробы на результат последующего измерения другой пробы того же материала. В этом случае результаты эксперимента по оценке прецизионности будут искажены: оценки стандартного отклонения повторяемости sr будут уменьшены, а оценки межлабораторного стандартного отклонения sL возрастут. В эксперименте с разделенными уровнями каждую лабораторию - участницу эксперимента снабжают двумя подобными пробами материала для каждого уровня эксперимента, а операторам сообщают, что пробы не идентичны, но не информируют о степени их различия. Эксперимент с разделенными уровнями обеспечивает, таким образом, возможность определения стандартных отклонений повторяемости и воспроизводимости стандартного метода измерений способом, снижающим риск воздействия результата измерений, полученного на одной пробе, на результат измерений, полученный в эксперименте на другой пробе.
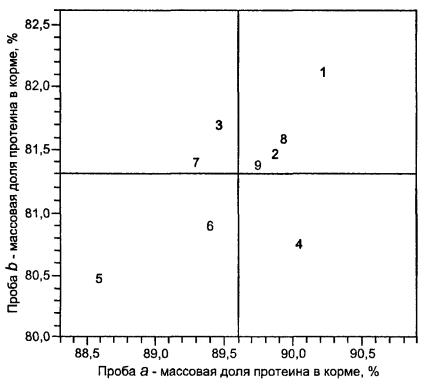
4.1.2 Данные, полученные на одном уровне в эксперименте с разделенными уровнями, можно представить на графике, в котором данные для одной пробы материала наносят против данных для другой пробы, относящейся к тому же уровню. Пример дан на рисунке 1. Такие графики могут помочь идентифицировать те лаборатории, которые имеют наибольшие систематические погрешности относительно других лабораторий, и исследовать источники наибольших лабораторных систематических погрешностей с целью принятия корректирующих действий.
4.1.3 В общем случае стандартные отклонения повторяемости и воспроизводимости метода измерений зависят от уровня измеряемой характеристики материала. Например, когда результат измерений пропорционален определяемому содержанию элемента, стандартные отклонения повторяемости и воспроизводимости обычно возрастают пропорционально возрастанию содержания элемента. Для эксперимента с разделенными уровнями необходимо, чтобы две пробы материала, используемые на одном уровне эксперимента, были настолько подобны, чтобы можно было ожидать тех же стандартных отклонений повторяемости и воспроизводимости. При этом для целей эксперимента с разделенными уровнями приемлемо, если две пробы материала, используемые на одном уровне, дают почти одинаковые результаты измерений, и не следует добиваться, чтобы эти результаты существенно отличались.
Во многих химических аналитических методах матрица с содержанием анализируемого вещества может влиять на прецизионность, тогда как для эксперимента с разделенными уровнями требуются для каждого уровня две пробы материала с одинаковыми матрицами. Подобная проба материала может иногда быть приготовлена путем добавки интересующего нас вещества. Для материалов природного или промышленного происхождения может быть трудно найти два достаточно подобных продукта, необходимых для эксперимента с разделенными уровнями: в этом случае возможным решением является использование раствора, полученного на основе двух партий одного и того же продукта. Необходимо помнить, что целью выбора материалов для эксперимента с разделенными уровнями является обеспечение операторов пробами, от эксперимента с которыми не ожидают идентичности.
4.2 План эксперимента
4.2.1 План эксперимента с разделенными уровнями показан в таблице 1.
Число лабораторий-участниц р, каждая из которых испытывает по две пробы на q уровнях.
Две пробы внутри уровня обозначены а (проба одного материала) и b (проба другого, подобного материала).
4.2.2 Данные эксперимента с разделенными уровнями обозначают yijk, где i - номер лаборатории (i = 1, 2, ..., р); j - уровень (j = 1, 2, ..., q); k - проба (k = а или b).
4.3 Организация эксперимента
4.3.1 Руководство по планированию эксперимента с разделенными уровнями приведено в разделе 6 ГОСТ Р ИСО 5725-1. Подраздел 6.3 ГОСТ Р ИСО 5725-1 содержит формулы (использующие величину, обозначенную буквой А), необходимые для принятия решений о числе лабораторий, привлекаемых к участию в эксперименте. Соответствующие формулы для эксперимента с разделенными уровнями приведены ниже.
Примечание - Формулы получены методом, описанным в примечании 24 ГОСТ Р ИСО 5725-1.
Для аналитического выражения неопределенности оценок стандартных отклонений повторяемости и воспроизводимости используют следующие равенства.
Для повторяемости
Для воспроизводимости
где g = sR/sr.
При п = 2 формулы (1) и (2) совпадают с формулами (9) и (10) ГОСТ Р ИСО 5725-1, за исключением того, что в них вместо р из ГОСТ Р ИСО 5725-1 появляется р - 1. Это небольшая разница, так что для представления неопределенности оценок стандартных отклонений повторяемости и воспроизводимости в эксперименте с разделенными уровнями могут быть использованы таблица 1 и рисунки В.1 и В.2 ГОСТ Р ИСО 5725-1.
Неопределенность оценки систематической погрешности метода измерений в эксперименте с разделенными уровнями рассчитывают в соответствии с формулой (13) из ГОСТ Р ИСО 5725-1 для п = 2 или определяют непосредственно из таблицы 2 ГОСТ Р ИСО 5725-1.
Неопределенность оценки лабораторной систематической погрешности в эксперименте с разделенными уровнями рассчитывают по уравнению (16) ГОСТ Р ИСО 5725-1 для п = 2. Поскольку число параллельных определений в эксперименте с разделенными уровнями равно двум, это не позволяет уменьшить неопределенность оценки лабораторной систематической погрешности увеличением числа параллельных определений. (Если необходимо снизить эту неопределенность, то необходимо использовать эксперимент с однородными уровнями).
4.3.2 Следуя руководству, приведенному в разделах 5 и 6 ГОСТ Р ИСО 5725-2, следует отнестись с вниманием к деталям организации эксперимента с разделенными уровнями. Число параллельных определений и в ГОСТ Р ИСО 5725-2 должно быть равным числу параллельных определений в эксперименте с разделенными уровнями, то есть двум.
Пробы а и b должны быть распределены среди участников случайным образом, причем процедуры рандомизации для а и b должны быть независимы. При этом необходимо, чтобы эксперты-статистики имели точную информацию о том, какие результаты были получены на материале а и какие - на материале b на каждом уровне эксперимента. Однако пробы следует зашифровать так, чтобы скрыть эту информацию от участников эксперимента.
Таблица 1 - Рекомендуемая форма для сравнения данных эксперимента с разделенными уровнями
|
Уровень |
||||||||||
|
1 |
2 |
|
j |
|
q |
|||||
|
а |
b |
а |
b |
|
а |
b |
|
а |
b |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
4.4 Статистическая модель
4.4.1 Основная модель, используемая в настоящем стандарте, дана равенством (1) в разделе 5 ГОСТ Р ИСО 5725-1. Там установлено, что для оценивания точности (правильности и прецизионности) метода измерений каждый результат измерения полезно представлять как сумму трех составляющих:
yijk = mj + Bij + eijk, (3)
где для определенного испытуемого материала:
mj - общее среднее значение для определенного уровня j = 1, ..., q;
Bij - лабораторная составляющая систематической погрешности в условиях повторяемости в определенной лаборатории i = 1, ..., р на определенном уровне j = 1, ..., q;
eijk - случайная погрешность результата измерений k = 1, ..., п, полученная в лаборатории i на уровне j в условиях повторяемости.
4.4.2 Для эксперимента с разделенными уровнями эта модель принимает вид
yijk = mjk + Bij + eijk. (4)
Это неравенство отличается от равенства (3) только одной деталью: индекс k в mjk означает, что в соответствии с равенством (4) общее среднее значение может теперь зависеть от материала а или b (k = 1 или 2) на уровне j.
Отсутствие индекса k в Вij означает допущение, что систематическая ошибка, связанная с лабораторией i, не зависит от материала а или b на определенном уровне. Вот почему так важно, чтобы эти два материала были бы однородными (одинаковыми).
4.4.3 Определяют среднее значение в базовом элементе (ячейке)
yij = (yija + yijb)/2 (5)
и внутриэлементное расхождение (разброс)
Dij = yija - yijb. (6)
4.4.4 Общее среднее значение для уровня j в эксперименте с разделенными уровнями может быть определено как
mj = (mja + mjb)/2. (7)
4.5 Статистический анализ данных эксперимента с разделенными уровнями
4.5.1 Данные эксперимента сводят в таблицу (см. таблицу 1). Каждая комбинация лаборатории и уровня дает базовый элемент (ячейку) в этой таблице, а также содержит два результата yija и yijb.
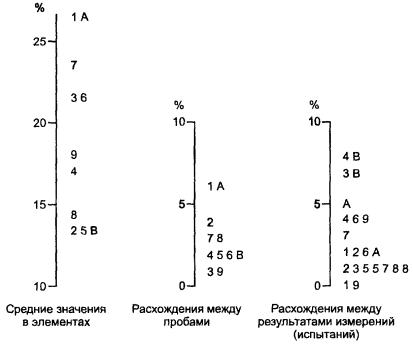
Рассчитывают Dij - расхождения в элементах и сводят их в таблицу (см. таблицу 2). Метод анализа требует, чтобы все расхождения были рассчитаны с сохранением знака разности
а - b.
Рассчитывают средние значения уij и сводят их в таблицу (см. таблицу 3).
4.5.2 Если элемент в таблице 1 не содержит двух результатов измерений (например потому, что пробы были испорчены или данные исключены в последующем как выбросы), то соответствующие элементы в таблицах 2 и 3 оставляют пустыми.
4.5.3 Для каждого уровня j эксперимента рассчитывают среднее Dj и стандартное sDj отклонения расхождений в графе j таблицы 2 по формулам:
где Σ - знак суммирования по всем лабораториям i = 1, 2, ..., р.
Если в таблице 2 имеются пустые элементы, то р теперь становится числом элементов в графе j таблицы 2, содержащих данные, и суммирование выполняют без пустых элементов.
4.5.4 Для каждого уровня j в эксперименте рассчитывают среднее и стандартное отклонения средних значений в графе j таблицы 3, используя формулы:
где Σ - знак суммирования по всем лабораториям i = 1, 2, ..., р.
Если в таблице 3 имеются пустые элементы, то р теперь становится числом элементов в графе j, содержащих данные, и суммирование выполняют без пустых элементов.
4.5.5 Для проверки совместимости данных и наличия выбросов, как описано в 4.6, используют таблицы 2, 3 и статистики, рассчитанные по формулам (8-11). При исключении данных пересчитывают статистики.
4.5.6 Рассчитывают стандартные отклонения повторяемости srj и воспроизводимости sRj по формулам:
4.5.7 Исследуют, зависят ли srj и sRj от среднего уj и, если это так, находят соответствующие функциональные соотношения, используя методы, описанные в 7.5 ГОСТ Р ИСО 5725-2.
Таблица 2 - Рекомендуемая форма табулирования расхождений в базовых элементах для эксперимента с разделенными уровнями
|
Уровень |
||||||
|
1 |
2 |
|
j |
|
q |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
Таблица 3 - Рекомендуемая форма табулирования средних значений в базовых элементах для эксперимента с разделенными уровнями
|
Уровень |
||||||
|
1 |
2 |
|
j |
|
q |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
p |
|
|
|
|
|
|
4.6 Исследование данных на совместимость и наличие выбросов
4.6.1 Проверяют данные на совместимость, используя статистику h, описанную в 7.3.1 ГОСТ Р ИСО 5725-2.
Чтобы проконтролировать совместимость расхождений в базовых элементах, рассчитывают серию для статистики h по формуле
hij = (Dij - Dj)/sDj. (14)
Для контроля совместимости средних значений в базовых элементах рассчитывают серию для статистики h по формуле
hij = (yij - yj)/syj. (15)
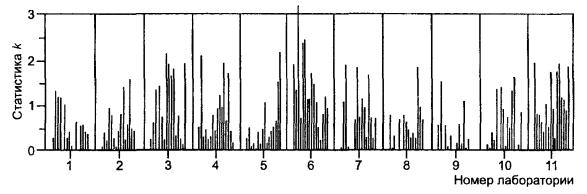
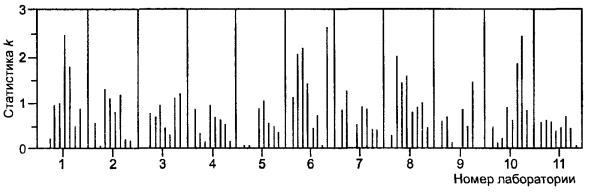
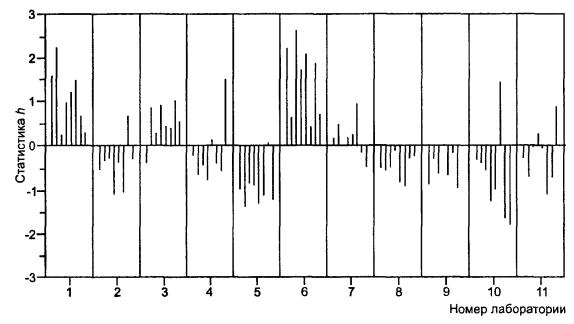
Для оценки различий лабораторий с точки зрения совместимости полученных данных, наносят на график обе серии в порядке возрастания уровней, но сгруппировав их по лабораториям, как показано на рисунках 2 и 3. Интерпретация этих графиков подробно рассмотрена в 7.3.1 ГОСТ Р ИСО 5725-2. Если лаборатория получила худшую повторяемость по сравнению с другими, это будет видно по необычно большому числу больших значений h на графике, построенном по расхождениям в элементах. Если данные лаборатории, в основном, содержат систематическую погрешность, то это будет видно по значениям h на графике, построенном для средних значений в элементах: большинство из них расположится в одном направлении. В любом случае лаборатория должна изучить причины расхождений и доложить о них организатору эксперимента.
4.6.2 Для контроля данных на наличие квазивыбросов и выбросов используют критерий Граббса, описанный в 7.3.4 ГОСТ Р ИСО 5725-2.
Для контроля наличия квазивыбросов и выбросов во внутриэлементных расхождениях, применяют тестирование по критерию Граббса к значениям в каждой графе таблицы 2 по очереди.
Для контроля наличия квазивыбросов и выбросов в средних значениях элементов применяют тестирование по критерию Граббса к значениям в каждой графе таблицы 3 по очереди.
Интерпретация результатов тестирования полностью рассмотрена в 7.3.2 ГОСТ Р ИСО 5725-2. Их используют для идентификации результатов, которые настолько не соответствуют остальным данным эксперимента, что в случае их включения в расчеты стандартных отклонений повторяемости и воспроизводимости они окажут существенное влияние на значения этих статистик. Обычно данные, идентифицированные как выбросы, исключают из расчетов, а данные, идентифицированные как квазивыбросы, включают в расчеты, если не имеется серьезных оснований для принятия других решений. Если результаты тестирования показывают, что данные в одной из таблиц 2 или 3 должны быть исключены из расчетов стандартных отклонений повторяемости и воспроизводимости, то соответствующие значения в другой таблице также должны быть исключены.
4.7 Представление результатов эксперимента
4.7.1 В 7.7 ГОСТ Р ИСО 5725-2 даны рекомендации по:
- созданию совета экспертов специально для организации эксперимента и рассмотрения его результатов;
- представлению результатов статистического анализа совету экспертов;
- решениям, принимаемым советом экспертов по результатам рассмотрения;
- подготовке полного отчета.
4.7.2 Рекомендации по форме представления установленных стандартных отклонений повторяемости и воспроизводимости стандартного метода измерений даны в 7.1 ГОСТ Р ИСО 5725-1.
4.8 Пример 1. Эксперимент с разделенными уровнями
4.8.1 Таблица 4 содержит данные эксперимента [2] по определению содержания протеина в кормах методом сжигания. Число лабораторий-участниц - девять, эксперимент содержал 14 уровней. В каждом уровне использовались две пробы кормов с одинаковой массовой долей протеина.
Таблица 4 - Пример 1. Определение массовой доли протеина в кормах (в процентах)
|
Уровень |
||||||||||||||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|||||||||||||||
|
а |
b |
а |
b |
а |
b |
а |
b |
а |
b |
а |
b |
а |
b |
а |
b |
а |
b |
а |
b |
а |
b |
а |
b |
а |
b |
а |
b |
|
|
1 |
11,11 |
10,34 |
10,91 |
9,81 |
13,74 |
13,48 |
13,79 |
13,00 |
15,89 |
15,26 |
20,14 |
19,78 |
20,33 |
20,06 |
46,45 |
44,42 |
52,05 |
49,40 |
65,84 |
59,14 |
84,16 |
80,86 |
85,38 |
81,71 |
87,64 |
88,23 |
90,24 |
82,10 |
|
2 |
11,12 |
9,94 |
11,38 |
10,31 |
14,00 |
13,12 |
13,44 |
13,06 |
15,69 |
15,10 |
19,25 |
20,25 |
20,36 |
19,94 |
46,69 |
44,62 |
51,94 |
48,81 |
66,31 |
59,19 |
84,50 |
81,06 |
85,56 |
82,44 |
88,81 |
88,38 |
89,88 |
81,44 |
|
3 |
11,26 |
10,46 |
10,95 |
10,51 |
13,38 |
12,70 |
13,54 |
13,18 |
15,83 |
15,73 |
20,48 |
19,86 |
20,56 |
20,11 |
46,90 |
44,56 |
52,18 |
48,90 |
66,06 |
58,52 |
82,26 |
79,43 |
85,26 |
82,15 |
88,58 |
88,12 |
89,48 |
81,67 |
|
4 |
11,07 |
10,41 |
11,66 |
9,95 |
13,01 |
13,16 |
13,58 |
12,88 |
15,08 |
15,63 |
21,54 |
20,06 |
20,64 |
20,46 |
47,13 |
45,29 |
51,73 |
48,56 |
65,93 |
58,93 |
84,39 |
80,08 |
85,20 |
81,76 |
88,47 |
87,98 |
90,04 |
80,73 |
|
5 |
10,69 |
10,31 |
10,98 |
10,13 |
13,24 |
13,33 |
13,32 |
12,59 |
15,02 |
14,90 |
19,90 |
19,66 |
20,56 |
19,24 |
45,83 |
43,73 |
50,84 |
47,91 |
64,19 |
57,94 |
81,71 |
79,01 |
83,58 |
79,74 |
86,43 |
86,19 |
88,59 |
80,46 |
|
6 |
11,73 |
11,01 |
12,31 |
10,92 |
14,01 |
13,66 |
14,04 |
13,64 |
16,43 |
15,94 |
20,31 |
20,27 |
20,85 |
20,63 |
46,86 |
43,96 |
52,18 |
49,03 |
65,73 |
58,77 |
82,85 |
81,16 |
84,44 |
80,90 |
87,78 |
86,89 |
89,40 |
80,88 |
|
7 |
11,13 |
10,36 |
11,38 |
10,44 |
12,94 |
12,44 |
13,63 |
13,06 |
15,75 |
15,56 |
20,00 |
20,56 |
20,25 |
20,19 |
46,25 |
44,31 |
52,25 |
49,44 |
66,06 |
59,19 |
86,25 |
81,00 |
84,88 |
81,44 |
88,06 |
88,00 |
89,31 |
81,38 |
|
8 |
11,21 |
10,51 |
11,32 |
10,84 |
13,09 |
13,76 |
13,85 |
13,49 |
15,98 |
15,89 |
20,43 |
20,69 |
20,85 |
20,27 |
47,11 |
44,40 |
52,44 |
48,81 |
65,66 |
59,38 |
84,59 |
81,16 |
84,96 |
81,71 |
88,50 |
87,98 |
89,94 |
81,56 |
|
9 |
11,80 |
11,21 |
11,35 |
9,88 |
13,85 |
14,46 |
13,96 |
13,77 |
16,51 |
15,72 |
20,64 |
21,01 |
20,78 |
20,89 |
47,09 |
45,15 |
52,19 |
48,46 |
66,33 |
59,47 |
83,05 |
80,93 |
84,73 |
81,94 |
88,24 |
88,05 |
89,75 |
81,35 |
4.8.2 Таблицы 5 и 6 содержат средние значения и внутриэлементные расхождения, рассчитанные, как описано в 4.5.1, только для уровня 14 (j = 14) этого эксперимента.
Использование уравнений (8) и (9) по 4.5.3 для определения расхождений, приведенных в таблице 5, дает:
D14 = 8,34 %,
sD14 = 0,4361 %,
а применяя уравнения (10) и (11) в 4.5.4 к средним значениям, приведенным в таблице 6, получим:
у14 = 85,46 %,
s14 = 0,4534 %,
и тогда стандартные отклонения повторяемости и воспроизводимости, согласно уравнениям (12) и (13), равны:
sr14 = 0,31 %,
sR14 = 0,50 %.
Таблица 5 - Пример 1. Расхождения в элементах для уровня 14
|
Расхождение, % |
Статистика h |
|
|
1 |
8,14 |
-0,459 |
|
2 |
8,44 |
0,229 |
|
3 |
7,81 |
-1,215 |
|
4 |
9,31 |
2,224 |
|
5 |
8,13 |
-0,482 |
|
6 |
8,52 |
0,413 |
|
7 |
7,93 |
-0,940 |
|
8 |
8,38 |
0,092 |
|
9 |
8,40 |
0,138 |
Таблица 6 - Пример 1. Средние значения в элементах для уровня 14
|
Расхождение, % |
Статистика h |
|
|
1 |
86,170 |
1,576 |
|
2 |
85,660 |
0,451 |
|
3 |
85,575 |
0,263 |
|
4 |
85,385 |
-0,156 |
|
5 |
84,525 |
-2,052 |
|
6 |
85,140 |
-0,696 |
|
7 |
85,345 |
-0,244 |
|
8 |
85,750 |
0,649 |
|
9 |
85,550 |
0,208 |
Таблица 7 дает результаты расчетов и для других уровней.
Таблица 7 - Пример 1. Средние значения, средние расхождения и стандартные отклонения, рассчитанные по данным для 14 уровней из таблицы 4
|
Уровень j |
Число лабораторий р |
Общее среднее значение уj, % |
Среднее расхождение Dj, % |
Стандартные отклонения, % |
|||
|
syj |
sDj |
srj |
sRj |
||||
|
1 |
9 |
10,87 |
0,73 |
0,35 |
0,21 |
0,15 |
0,36 |
|
2 |
9 |
10,84 |
1,05 |
0,36 |
0,43 |
0,30 |
0,42 |
|
3 |
9 |
13,41 |
0,13 |
0,44 |
0,55 |
0,39 |
0,52 |
|
4 |
9 |
13,43 |
0,50 |
0,30 |
0,21 |
0,15 |
0,32 |
|
5 |
9 |
15,66 |
0,27 |
0,39 |
0,40 |
0,29 |
0,44 |
|
6 |
9 |
20,27 |
0,06 |
0,40 |
0,73 |
0,52 |
0,54 |
|
7 |
9 |
20,39 |
0,38 |
0,30 |
0,41 |
0,29 |
0,37 |
|
8 |
9 |
45,60 |
2,21 |
0,44 |
0,37 |
0,26 |
0,47 |
|
9 |
9 |
50,40 |
3,16 |
0,44 |
0,35 |
0,25 |
0,47 |
|
10 |
9 |
62,37 |
6,84 |
0,53 |
0,40 |
0,28 |
0,57 |
|
11 |
9 |
82,14 |
3,23 |
1,01 |
1,08 |
0,77 |
1,15 |
|
12 |
9 |
83,17 |
3,45 |
0,74 |
0,46 |
0,33 |
0,77 |
|
13 |
9 |
87,91 |
0,30 |
0,69 |
0,41 |
0,29 |
0,72 |
|
14 |
9 |
85,46 |
8,34 |
0,45 |
0,44 |
0,31 |
0,50 |
4.8.3 На рисунке 1 для уровня 14 представлены результаты для проб а из таблицы 4, расположенных напротив соответствующих результатов, полученных для проб b, в виде так называемой диаграммы Юдена («Youden plot»). Лаборатория № 5 дает точку в нижнем левом углу рисунка, а лаборатория № 1 - в верхнем правом углу. Это означает, что лаборатория № 5 имеет согласованную отрицательную систематическую погрешность по пробам а и b; данные лаборатории № 1 имеют согласованную положительную систематическую погрешность по двум пробам. Представление данных эксперимента с разделенными уровнями в виде подобных диаграмм является обычным для нахождения таких отклонений (как показано на рисунке 1). Рисунок также показывает, что результаты лаборатории № 4 необычны, так как точка этой лаборатории сравнительно далеко отстоит от линии равенства (баланса) для двух проб. Другие лаборатории формируют группу результатов в середине графика. Этот рисунок, таким образом, указывает, что целесообразно исследовать источники систематических погрешностей в трех лабораториях.
Примечание - Относительно интерпретации диаграмм Юдена, см. [2] и [3].
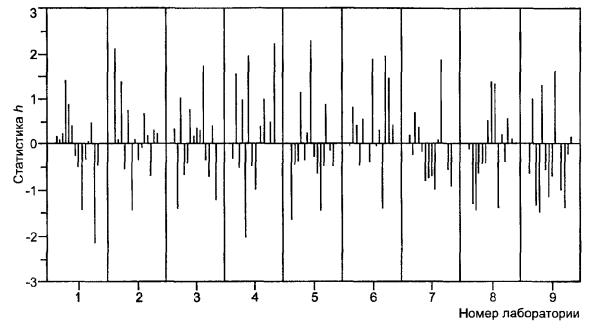
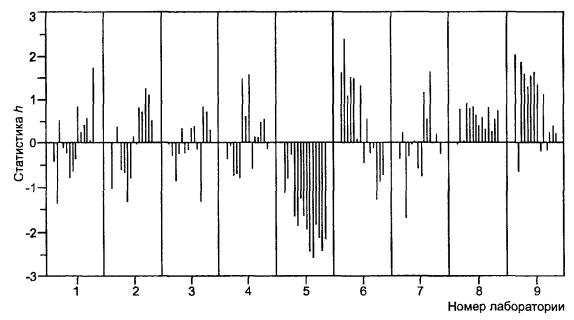
4.8.4 Значения статистики h, рассчитанные согласно 4.6.1, представлены в таблицах 5 и 6 только для уровня 14. Значения для всех остальных уровней представлены на рисунках 2 и 3.
Из рисунка 3, где представлена статистика h для средних значений элементов, видно, что лаборатория № 5 дала отрицательные значения статистики h на всех уровнях, что указывает на согласованную отрицательную систематическую погрешность ее данных. На этом же рисунке значения статистики h для лабораторий № 8 и № 9 почти всегда положительны, что указывает на согласованные положительные систематические погрешности их данных (меньшие, чем отрицательная систематическая погрешность в лаборатории № 5). Для лабораторий № 1, 2 и 6 статистика h свидетельствует о том, что в каждой из этих лабораторий систематическая погрешность изменяется в зависимости от уровня. Такая взаимосвязь между лабораториями и уровнями может стать ключом к пониманию источников лабораторных систематических погрешностей.
Рисунок 2 не обнаруживает достойных внимания отклонений или зависимостей.
4.8.5 Значения статистики Граббса даны в таблице 8. Эти данные вновь свидетельствуют, что результаты, полученные от лаборатории № 5, сомнительны.
4.8.6 На этом этапе анализа эксперт по статистике должен инициировать исследования в лаборатории № 5 по поиску возможных причин получения сомнительных данных перед дальнейшим анализом. Если причина не может быть установлена, то в этом случае целесообразно исключить все данные лаборатории № 5 из расчетов стандартных отклонений повторяемости и воспроизводимости. Анализ потом можно продолжить в направлении исследования возможной функциональной зависимости между стандартными отклонениями повторяемости и воспроизводимости и общим средним (по уровню). Этот вопрос рассмотрен уже в ГОСТ Р ИСО 5725-2, поэтому здесь он не рассматривается.
Таблица 8 - Пример 1. Значения статистики Граббса
|
Статистика Граббса для расхождений |
Статистика Граббса для средних значений |
|||||||||
|
Одно наименьшее |
Два наименьших |
Два наибольших |
Одно наибольшее |
Одно наименьшее |
Два наименьших |
Два наибольших |
Одно наибольшее |
|||
|
1 |
1,653 |
0,5081 |
0,3139 |
2,125 |
1,070 |
0,6607 |
0,1291* (6; 9) |
1,832 |
||
|
2 |
1,418 |
0,3945 |
0,4738 |
1,535 |
1,318 |
0,6288 |
0,2118 |
2,165 |
||
|
3 |
1,462 |
0,3628 |
0,5323 |
1,379 |
1,621 |
0,4771 |
0,4077 |
1,680 |
||
|
4 |
1,490 |
0,5841 |
0,4771 |
1,414 |
1,591 |
0,5339 |
0,3807 |
1,429 |
||
|
5 |
2,033 |
0,3485 |
0,6075 |
1,289 |
1,794 |
0,4018 |
0,5009 |
1,333 |
||
|
6 |
1,456 |
0,5490 |
0,3210 |
1,947 |
1,291 |
0,4947 |
0,4095 |
1,386 |
||
|
7 |
1,185 |
0,6820 |
0,1712 |
2,296* (5) |
1,599 |
0,5036 |
0,4391 |
1,470 |
||
|
8 |
0,996 |
0,7571 |
0,1418* (6; 8) |
1,876 |
1,872 |
0,3753 |
0,4536 |
1,404 |
||
|
9 |
1,458 |
0,5002 |
0,3092 |
1,602 |
2,328* (5) |
0,1317* (4; 5) |
0,7417 |
1,025 |
||
|
10 |
1,474 |
0,3360 |
0,4578 |
1,737 |
2,456** (5) |
- |
- |
1,000 |
||
|
11 |
1,422 |
0,5089 |
0,2943 |
1,865 |
1,756 |
0,2469 |
0,5759 |
1,472 |
||
|
12 |
1,418 |
0,6009 |
0,2899 |
1,956 |
2,037 |
0,1063* (5; 6) |
0,7116 |
1,130 |
||
|
13 |
2,172 |
0,2325 |
0,6326 |
1,444 |
2,308* (5) |
0,0733** (5; 6) |
0,7777 |
0,994 |
||
|
14 |
1,215 |
0,6220 |
0,2362 |
2,224* (4) |
2,052 |
0,2781 |
0,5486 |
1,576 |
||
|
Примечание - в скобках указаны номера лабораторий, давших квазивыбросы или выбросы. Ниже приведены критические значения статистики Граббса для девяти лабораторий, применяемые как к расхождениям, так и к средним значениям. |
||||||||||
|
|
* Квазивыброс |
** Выброс |
||||||||
|
Для одного выброса |
2,215 0 |
2,387 0 |
||||||||
|
Для пары выбросов |
0,149 2 |
0,085 1 |
||||||||
Рисунок 1 - Пример 1. Данные, полученные на уровне 14
Рисунок 2 - Пример 1. Проверка совместимости по внутриэлементным расхождениям (сгруппированным по лабораториям)
Рисунок 3 - Пример 1. Проверка совместимости по средним значениям в элементах (сгруппированным по лабораториям)
5 Модель эксперимента для гетерогенного материала
5.1 Применение модели
5.1.1 Примером гетерогенного материала является кожа. Нет двух одинаковых шкур, а свойства кожи существенно меняются в пределах одной шкуры. Обычное испытание, которое применяют для кожи, это испытание на прочность по BS 3144 [4]. Испытание проводят на вырезанных из шкуры фрагментах (BS 3144 определяет число таких фрагментов, а также их расположение и ориентацию по шкуре так, чтобы естественным определением «пробы» при испытаниях кожи стала вся шкура). Если эксперимент по оценке прецизионности выполняют по модели с однородными уровнями, описанной в ГОСТ Р ИСО 5725-2, в соответствии с которой в каждую лабораторию посылают по одной шкуре для каждого уровня эксперимента и получают по два результата по каждой шкуре, то различия между шкурами будут добавляться к межлабораторной вариации, таким образом увеличивая стандартное отклонение воспроизводимости. Однако если в каждую лабораторию посылают по две шкуры для каждого уровня и получают два результата по каждой шкуре, то эти данные могут быть использованы для оценки расхождений между шкурами и по ним может быть рассчитано стандартное отклонение воспроизводимости метода испытаний, из значения которого различие между самими шкурами исключено.
5.1.2 Другим примером гетерогенного материала является гравий (который может быть использован, например, для производства бетона). Обычно под воздействием ветра или воды в нижнем пласте содержится гравий различных фракций, и их распределение по размеру представляет особый интерес. В технологии производства бетона распределение гравия по фракциям контролируют ситовым анализом (например, согласно BS 812-103 [5]). Для испытаний сначала отбирают пробу гравия определенного объема, затем из нее готовят одну или более порций для испытаний. Типичными являются проба массой около 10 кг и навески для испытаний около 200 г. Естественная неоднородность материала приводит всегда к некоторым различиям между объемами проб, отобранных из одного и того же продукта. Отсюда, по аналогии с кожей, если эксперимент проводят по модели с однородными уровнями, в каждую лабораторию посылают пробы одного объема для каждого уровня, и тогда расхождения между пробами будут увеличивать рассчитанное стандартное отклонение воспроизводимости метода испытаний, но если в лаборатории посылают по две пробы для каждого уровня, тогда значения стандартного отклонения воспроизводимости могут быть рассчитаны так, что эти различия между пробами будут исключены.
5.1.3 Вышеприведенные примеры также ставят на первый план характеристику неоднородности гетерогенных материалов, так как из-за неоднородности материала (образца) приготовленные для испытаний фрагменты или порции могут быть важным источником расхождений. Так, в примере с кожей процесс вырезки фрагментов шкуры может оказать заметное влияние на измеряемое усилие при вырезке. Аналогично при испытаниях гравия на сите процесс приготовления навесок для испытаний из всего объема пробы обычно является главным источником расхождений результатов. Если образцы или навески (пробы) готовят для эксперимента по оценке прецизионности с отклонениями от нормальной практики (в попытке приготовить идентичные «пробы»), то значения стандартных отклонений повторяемости и воспроизводимости, полученные в эксперименте, не будут представлять различие между образцами, имеющее место на практике. Иногда желательно приготовить «идентичные» пробы, чтобы исключить, насколько это возможно, неоднородность материала (например для квалификационного испытания или когда эксперимент по оценке прецизионности используют как часть программы по исследованию метода измерений). Однако, когда целью эксперимента по оценке прецизионности является установление расхождения, которое будет иметь место на практике (например, когда поставщик и покупатель испытывают пробы одного и того же продукта), тогда расхождение, возникающее вследствие гетерогенности материала, необходимо включать в оценку прецизионности метода измерений.
Необходимо также предусмотреть, чтобы каждый результат в эксперименте был получен с соблюдением процедуры испытаний, независимо от других испытаний. Это будет не так, если отдельные стадии приготовления образцов будут выполняться совместно для нескольких образцов таким образом, что систематические или случайные погрешности, обусловленные стадией приготовления образцов, будут иметь общее влияние на результаты испытаний, полученные на этих образцах.
5.1.4 Модель для гетерогенных материалов, предложенная в пункте 5.1, дает информацию о различиях между пробами, которые не могут быть получены по модели с однородными уровнями, описанной в ГОСТ Р ИСО 5725-2. Конечно, неизбежны расходы, связанные с получением дополнительной информации, так как предлагаемая модель требует большего количества проб для испытаний. Но эта дополнительная информация может быть ценной. В примере с кожей, рассмотренном в 5.1.1, информация о неоднородности шкур может быть использована для принятия решения о том, сколько шкур необходимо для испытаний при отправке товара, или же, что лучше - испытывать больше шкур с небольшим количеством фрагментов от каждой шкуры или испытывать шкур поменьше, но с бóльшим количеством фрагментов от каждой шкуры. В примере с гравием, рассмотренном в 5.1.2, информация о различиях между пробами может быть использована для решения, является ли процедура отбора проб из большого объема удовлетворительной или нуждается в совершенствовании.
5.1.5 Модель, описанная в этом пункте, применима к экспериментам, включающим три фактора, расположенных в такой последовательности: «лаборатории» - как высочайший уровень в иерархии, фактор «пробы внутри лабораторий» - как следующий уровень в иерархии и фактор «результаты испытаний в пределах проб» - самый низкий уровень в иерархии. Другой случай, с которым можно столкнуться на практике, - трехфакторная иерархия: «лаборатории» - как высочайший уровень, «результаты испытаний в пределах лабораторий» - как следующий уровень и «результаты параллельных определений в результатах испытаний» - как наинизший уровень. Этот случай может возникнуть, если лабораториям - участницам эксперимента по оценке прецизионности посылают по одной пробе гомогенного материала с просьбой о выполнении двух (возможно - более) испытаний на каждой пробе и если каждое испытание включает в себя некоторое число определений, а результаты испытаний рассчитывают как средние значения этих определений. К значениям, полученным в таком эксперименте, применимы формулы, приведенные в 5.5, 5.6 и 5.9, но стандартные отклонения повторяемости и воспроизводимости должны быть рассчитаны несколько иным способом, который приведен в примечании 2 к 5.5.5. Необходимо также правильно задавать число определений, подлежащих усреднению, для выдачи результата испытаний, так как это влияет на значения стандартных отклонений повторяемости и воспроизводимости.
5.2 План эксперимента
5.2.1 План эксперимента для гетерогенного материала представлен в таблице 9.
Каждую лабораторию из числа р, участвующую в эксперименте, обеспечивают двумя пробами на каждом из q уровней и получают два результата измерений по каждой пробе. Таким образом каждый элемент (ячейка) в эксперименте содержит четыре результата измерений (по два результата измерений для каждой из двух проб).
Эту простую модель можно обобщить на случай использования более чем двух проб на лабораторию и уровень или получение более чем двух результатов измерений по каждой пробе. Расчеты по более общей модели значительно сложнее, чем в случаях с двумя результатами измерений по каждой пробе или с двумя пробами на лабораторию и уровень. Однако принципы более общей модели остаются теми же, как и в случае простой модели, поэтому расчеты будут изложены здесь детально для простой модели. Формулы для расчетов стандартных отклонений повторяемости и воспроизводимости при использовании общей модели даны ниже в 5.9, а пример по их применению - в 5.10.
5.2.2 Данные эксперимента для гетерогенного материала обозначают yijtk, где i - номер лаборатории (i = 1, 2, ..., р´); j - уровень (j = 1, 2, ..., q); t - проба (t = 1, 2, ..., g); k - результат измерений (k = 1, 2, ..., n).
Обычно g = 2 и n = 2. В большинстве общих моделей g > 2 и n > 2 или оба - более двух.
Примечание - В ГОСТ Р ИСО 5725-1 и ГОСТ Р ИСО 5725-2 р используют как число лабораторий и как индекс в таблицах критических значений для критерия Кохрена: для модели эксперимента с однородными уровнями это одно и то же число. В модели для гетерогенного материала индекс для критерия Кохрена может быть кратен числу лабораторий, поэтому р´ используют здесь для обозначения числа лабораторий, а р - для индекса критерия Кохрена.
5.3 Организация эксперимента
5.3.1 При планировании эксперимента с гетерогенным материалом необходимо следовать руководству, изложенному в разделе 6 ГОСТ Р ИСО 5725-1. Дополнительный вопрос, который должен быть рассмотрен: сколько проб должно быть подготовлено для каждой лаборатории на каждом уровне?
Обычно с учетом затрат, потребуется две пробы для каждой лаборатории на каждом уровне.
Формулы, таблицы и рисунки в разделе 6 и приложении В ГОСТ Р ИСО 5725-1 могут быть использованы при выборе числа лабораторий, проб и параллельных определений, но с модификациями, изложенными в 5.3.2 до 5.3.5.
5.3.2 Неопределенность оценки стандартного отклонения повторяемости, полученной из эксперимента на гетерогенном материале, может быть оценена расчетом величины Аr (см. 6.3 ГОСТ Р ИСО 5725-1) по формуле
вместо определенной равенством (9) ГОСТ Р ИСО 5725-1. Однако вышеприведенная формула может быть получена заменой р в уравнении (9) ГОСТ Р ИСО 5725-1 на р´ ´ g. Значит, на рисунке В.1 данные для повторяемости под Аr в таблице 1 ГОСТ Р ИСО 5725-1 могут быть использованы для эксперимента с гетерогенным материалом внесением на рисунок или в таблицу величины p = р´ ´ g. В общем случае, когда g = 2, пробы, подготовленные для каждой лаборатории и каждого уровня, вносят в таблицу или на рисунок в ГОСТ Р ИСО 5725-1 с р = 2 р´.
Примечание - Формулы (16) для Аr и (17) для AR получены методом, описанным в примечании 24 ГОСТ Р ИСО 5725-1.
5.3.3 Неопределенность оценки стандартного отклонения воспроизводимости, полученной из эксперимента на гетерогенном материале, может быть оценена вычислением величины AR (см. 6.3 ГОСТ Р ИСО 5725-1) по формуле
вместо определенной уравнением (10) ГОСТ Р ИСО 5725-1,
где D1 = [ (g2 - 1) + (Ф2/g) + 1/ng]2/(p´ - 1);
D2 = [ (Ф2/g) + (l/ng)] 2/[p´(g - 1)];
D3 = 1/[р´ g (n - 1)];
Ф = sH/sr (sH определено в 5.4.1).
Поправка. ИУС 11-2003.
g = sR/sr. (18)
Величины Ф и g могут быть выведены из предварительных оценок стандартных отклонений sH, sR и sr, полученных в процессе стандартизации метода измерения.
5.3.4 Детальную организацию эксперимента с гетерогенным материалом осуществляют в соответствии с руководством, изложенным в разделах 5 и 6 ГОСТ Р ИСО 5725-2.
Подпункт 5.1.2 ГОСТ Р ИСО 5725-2 содержит требования для «группы из n испытаний» или «группы из п измерений» (например требование, что группа из п испытаний должна проводиться с соблюдением условий повторяемости). В эксперименте на гетерогенном материале эти требования относят к группе g ´ п испытаний в элементе, то есть ко всем испытаниям в одной лаборатории на одном уровне.
В эксперименте на гетерогенном материале число проб, которое должно быть приготовлено для каждого уровня, равно р´ ´ g (то есть 2 р´ в обычном случае, когда g = 2). Важно разместить эти р´ ´ g проб по лабораториям-участницам случайным образом.
5.4 Статистическая модель эксперимента с гетерогенным материалом
5.4.1 Основная модель, использованная в настоящем стандарте, описана в 4.1.1 равенством (3). Для эксперимента с гетерогенным материалом эта модель принимает вид
yijtk = mj + Bij + Hijt + eijtk. (19)
Члены т, В и е имеют те же значения, как и в равенстве (3), но равенство (19) содержит особый член Hijt, который означает различие между пробами (неоднородность проб), а индекс t - номер пробы в лабораториях (значения других индексов даны в 5.2.2).
Естественно полагать, что различие между пробами является случайной величиной, не зависящей от лаборатории, но оно может зависеть от уровня в эксперименте. Тогда член Нijt, имеет нулевое математическое ожидание и дисперсию
Var (Hijt) = s2Hj (20)
5.4.2 В обычном случае с двумя пробами для лаборатории и двумя результатами измерений для пробы (g = п = 2), определяют:
a) среднее для пробы и расхождения между результатами испытаний для лаборатории i, уровня j и пробы t (t = 1 или 2)
yijt = (yijt 1 + yijt 2)/2, (21)
wijt = | yijt 1 - yijt 2|; (22)
b) среднее для элемента и различие между пробами для лаборатории i и уровня j
yij = (yij 1 + yij 2)/2, (23)
wij = | yij 1 - yij 2|; (24)
с) общее среднее и стандартное отклонение средних для элементов на уровне j
где суммирование осуществляют по всем лабораториям i = 1, 2, ..., p´.
5.5 Статистический анализ данных эксперимента
5.5.1 В этом пункте детально рассматривают случай, когда для каждой лаборатории на каждом уровне приготовлены по две пробы и на каждой пробе получены два результата измерений (общий случай рассматривают в 5.9 и 5.10).
Группируют полученные данные в таблицу (см. таблицу 9). Каждая комбинация лаборатории и уровня образует «элемент» в этой таблице, содержащий четыре результата измерений.
Используя уравнения (21)-(26):
a) рассчитывают расхождения между результатами измерений и сводят их в таблицу (см. таблицу 10);
b) рассчитывают расхождения между пробами и сводят их в таблицу (см. таблицу 11);
c) рассчитывают средние для элементов и сводят их в таблицу (см. таблицу 12);
Записывают расхождения как положительные величины (то есть игнорируя знак).
Таблица 9 - Рекомендуемая форма для сопоставления данных эксперимента для гетерогенного материала
|
Номер пробы |
Уровень |
||||||||||
|
1 |
2 |
|
j |
|
q |
||||||
|
Номер результата измерений |
|||||||||||
|
1 |
2 |
1 |
2 |
|
1 |
2 |
|
1 |
2 |
||
|
1 |
1 |
|
|
|
|
|
|
||||
|
2 |
|||||||||||
|
2 |
1 |
|
|
|
|
|
|
||||
|
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
||||
|
i |
1 |
|
|
|
|
|
|
||||
|
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
||||
|
p´ |
1 |
|
|
|
|
|
|
||||
|
2 |
|||||||||||
Таблица 10 - Рекомендуемая форма для табулирования расхождений между результатами измерений в эксперименте для гетерогенного материала
|
Номер пробы |
Уровень |
||||||
|
1 |
2 |
|
j |
|
q |
||
|
1 |
1 |
|
|
|
|
|
|
|
2 |
|||||||
|
2 |
1 |
|
|
|
|
|
|
|
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
i |
1 |
|
|
|
|
|
|
|
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
p´ |
1 |
|
|
|
|
|
|
|
2 |
|||||||
Таблица 11 - Рекомендуемая форма для табулирования расхождений между пробами в эксперименте для гетерогенного материала
|
Уровень |
||||||
|
1 |
2 |
|
j |
|
q |
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p´ |
|
|
|
|
|
|
Таблица 12 - Рекомендуемая форма для табулирования средних значений по элементам в эксперименте для гетерогенного материала
|
Уровень |
||||||
|
1 |
2 |
|
j |
|
q |
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p´ |
|
|
|
|
|
|
5.5.2 Если элемент в таблице 9 содержит менее четырех результатов измерений (например, по причине порчи проб или исключения данных после применения методов контроля наличия выбросов, описанных ниже), тогда:
а) либо используют формулы для общего случая, приведенные ниже;
b) либо игнорируют все данные в элементе.
Альтернатива а) является предпочтительной. Выбор b) - бросовые данные, допускает применение простых формул.
5.5.3 Для каждого уровня j эксперимента рассчитывают:
a) сумму квадратов расхождений между результатами измерений в графе j таблицы 10 (суммируют по р´ лабораториям и двум пробам)
b) сумму квадратов расхождений между пробами в графе j таблицы 11 (суммируют все р лабораторий)
c) среднее значение и стандартное отклонение средних для элементов в графе j таблицы 12 с использованием уравнений (25) и (26).
5.5.4 Используют таблицы 10-12 и статистические результаты, рассчитанные по 5.5.3, чтобы оценить данные на однородность и наличие выбросов, как описано в 5.6. Если какие-то данные исключают, пересчитывают статистические результаты.
5.5.5 Рассчитывают стандартные отклонения повторяемости srj и воспроизводимости sRj, пользуясь формулами:
![]() . (30)
. (30)
Если это дает
sRj < srj, (31)
тогда устанавливают
sRj = srj. (32)
Рассчитывают оценку стандартного отклонения sHj, являющегося мерой расхождения между пробами, по формуле
Примечания
1 Может показаться интересным выполнить испытание на значимость, чтобы определить, является ли расхождение между пробами статистически значимым, однако это не является необходимой частью анализа. Некорректно использовать такое испытание, чтобы решить, можно ли пренебречь расхождением между пробами в анализе (так как результаты измерений в каждом элементе обрабатывают так, как если бы они все были получены на одной и той же пробе). Это внесло бы систематическую погрешность в оценку стандартного отклонения повторяемости, поскольку утверждение о том, что расхождение между пробами не является статистически значимым, не доказывает, что этим расхождением можно пренебречь.
2 В случае, описанном в 5.1.5 (когда имеются три фактора: «лаборатории», «испытания внутри лабораторий» и «параллельные определения при выполнении испытаний»), стандартные отклонения повторяемости и воспроизводимости должны рассчитываться по формулам:
![]() ,
, ![]() .
.
Эти формулы применяют, когда результаты испытаний рассчитывают как среднее результатов двух определений.
5.5.6 Исследуют зависимость srj и sRj, от общего среднего yi и, если она есть, определяют функциональные соотношения, используя методы, описанные в 7.5 ГОСТ Р ИСО 5725-2.
5.6 Исследование данных на совместимость и наличие выбросов
5.6.1 При проверке данных на совместимость используют статистики h и k, описанные в 7.3.1 ГОСТ Р ИСО 5725-2.
Для контроля совместимости средних значений в элементах рассчитывают статистику h по формуле
hij = (yij - yj)/syj. (34)
Наносят статистические данные на график, чтобы показать, в каких лабораториях имеет место несовместимость, выстраивают данные по уровням, а также группируют их по лабораториям.
Для контроля совместимости расхождений между пробами рассчитывают статистику k по формуле
![]() . (35)
. (35)
Наносят статистические данные на график, чтобы показать, в каких лабораториях имеет место несовместимость, выстраивают данные по уровням, а также группируют их по лабораториям.
Для контроля совместимости расхождений между результатами измерений, рассчитывают статистику k по формуле
![]() . (36)
. (36)
Наносят эти статистические данные на график, чтобы показать, в каких лабораториях имеет место несовместимость, выстраивают данные по уровням, а также группируют их по лабораториям.
Интерпретация графиков полностью описана в 7.3.1 ГОСТ Р ИСО 5725-2. Если лаборатория сообщает результаты с систематическими погрешностями, то для нее большинство данных по статистике h для средних значений в элементах на соответствующем графике будет большим и иметь одно направление. Если лаборатория не провела измерение внутри уровней с соблюдением условий повторяемости (и допустила наличие посторонних факторов, увеличивших расхождение между пробами), то на соответствующем графике для статистики k будут видны необычно большие статистические данные для расхождений между пробами. Если лаборатория имеет плохую повторяемость, это проявится на графике в виде необычно больших значений статистики k для расхождений между результатами измерений.
5.6.2 Исследуют данные эксперимента с точки зрения наличия квазивыбросов и выбросов по критериям Кохрена и Граббса, как это описано в 7.3.3 и 7.3.4 ГОСТ Р ИСО 5725-2.
Для проверки наличия квазивыбросов и выбросов в расхождениях между результатами измерений рассчитывают значения статистики Кохрена для каждого уровня j по формуле
![]() , (37)
, (37)
где wmax - наибольшее расхождение между результатами измерений wijt для уровня j.
Для пользования таблицей критических значений подпункта 8.1 ГОСТ Р ИСО 5725-2 следует в таблице найти ряд, соответствующий р = 2р´, на краю слева и в графе п = 2.
Чтобы проверить наличие квазивыбросов и выбросов в расхождениях между пробами, рассчитывают значения статистики Кохрена для каждого уровня j по формуле
![]() , (38)
, (38)
где wmax - теперь наибольшее расхождение между пробами wij для уровня j.
Для пользования таблицей критических значений в ГОСТ Р ИСО 5725-2 следует в таблице найти ряд, соответствующий р = р´, на краю слева и в графе п = 2.
Чтобы проверить на наличие квазивыбросов и выбросов средние значения в элементах для каждого уровня j, рассчитывают по этим значениям статистику Граббса, как это показано в 7.3.4 ГОСТ Р ИСО 5725-2 (где s - это syj, определенное формулой (26) согласно 5.4.2).
Интерпретация этих проверок полностью описана в 7.3.2 ГОСТ Р ИСО 5725-2. В эксперименте на гетерогенном материале результаты этих проверок должны быть использованы в следующем порядке. Сначала нужно применить тест Кохрена к расхождениям между результатами измерений. Если на основе этого анализа решено, что расхождение между результатами измерений является выбросом и должно быть исключено, тогда оба результата измерений, которые дали выброс, должны быть исключены при расчетах стандартных отклонений повторяемости и воспроизводимости (но при этом другие результаты измерений в элементе должны быть оставлены). Далее применяют тест Кохрена к расхождениям между пробами и, наконец, - тесты Граббса к средним значениям в элементах. Если решено, что расхождение между пробами или среднее значение в элементе является выбросом и что результаты, которые стали источником таких выбросов, подлежат исключению, тогда все экспериментальные данные для соответствующих элементов исключают из расчетов стандартных отклонений повторяемости и воспроизводимости.
5.7 Представление результатов эксперимента
Рекомендации, предложенные в 4.7, в равной степени применимы к эксперименту на гетерогенном материале.
5.8 Пример 2. Эксперимент на гетерогенном материале
5.8.1 Агрегатированные частицы материалов (связанный цемент или битум), служащие для покрытия аэродромов и дорог, должны обладать определенной влаго- и морозостойкостью. Метод, который применяют для измерения этих их возможностей, - это испытание на прочность с использованием сульфата магния согласно BS 812-12 [6], при котором испытуемую навеску материала подвергают пропитке (в несколько циклов) в насыщенном растворе сульфата магния с последующей сушкой. Изначально навеску готовят из остатка на сите с отверстиями 10 мм после отсева. В процессе испытаний частицы измельчают, и результатом измерения является массовая доля от испытуемой навески, которая проходит через сито с отверстиями 10 мм. Высокий результат (свыше 10 % до 20 % по массе) означает агрегатное состояние с плохой прочностью.
Таблица 13 - Пример 2. Определение прочности с помощью сульфата магния, %
|
Номер пробы |
Уровень |
||||||||||||||||
|
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
||||||||||
|
Номер результата измерений |
|||||||||||||||||
|
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
||
|
1 |
1 |
69,2 |
67,0 |
7,4 |
8,0 |
4,1 |
3,5 |
10,4 |
10,1 |
8,9 |
7,4 |
31,1 |
28,5 |
38,7 |
41,7 |
4,2 |
4,1 |
|
2 |
69,7 |
71,7 |
6,6 |
5,7 |
10,5 |
13,1 |
13,9 |
13,8 |
7,6 |
9,1 |
23,0 |
23,1 |
44,2 |
41,1 |
7,3 |
4,4 |
|
|
2 |
1 |
66,5 |
64,1 |
1,9 |
2,1 |
3,0 |
3,2 |
8,7 |
6,7 |
3,2 |
3,5 |
16,5 |
15,4 |
36,6 |
45,2 |
3,2 |
5,4 |
|
2 |
65,7 |
65,8 |
4,2 |
3,3 |
1,9 |
1,1 |
8,3 |
4,8 |
2,8 |
4,0 |
10,3 |
12,8 |
43,2 |
40,5 |
1,7 |
2,5 |
|
|
3 |
1 |
68,7 |
69,5 |
6,3 |
5,8 |
2,4 |
2,9 |
11,7 |
7,0 |
4,4 |
6,1 |
24,3 |
16,7 |
38,9 |
43,1 |
3,7 |
7,7 |
|
2 |
67,7 |
77,7 |
9,7 |
5,3 |
2,1 |
3,3 |
7,9 |
12,0 |
6,0 |
6,0 |
20,8 |
22,2 |
46,1 |
47,4 |
3,5 |
5,6 |
|
|
4 |
1 |
77,5 |
75,3 |
2,0 |
3,6 |
2,4 |
1,4 |
9,4 |
7,1 |
2,7 |
3,1 |
20,2 |
16,2 |
32,0 |
35,5 |
2,9 |
2,2 |
|
2 |
76,3 |
77,2 |
4,7 |
3,8 |
6,4 |
2,3 |
10,7 |
7,7 |
2,3 |
2,9 |
20,0 |
11,9 |
26,5 |
35,7 |
3,2 |
2,3 |
|
|
5 |
1 |
55,4 |
63,2 |
3,8 |
4,1 |
1,3 |
0,8 |
3,7 |
6,3 |
1,3 |
1,4 |
13,8 |
15,1 |
36,7 |
39,5 |
1,1 |
1,2 |
|
2 |
65,9 |
54,7 |
2,1 |
3,1 |
0,7 |
1,7 |
3,3 |
3,7 |
1,5 |
1,3 |
11,5 |
13,3 |
37,6 |
34,1 |
0,6 |
1,7 |
|
|
6 |
1 |
64,8 |
70,9 |
8,4 |
6,1 |
6,0 |
9,7 |
16,5 |
12,3 |
8,2 |
4,2 |
20,3 |
24,7 |
49,4 |
50,6 |
11,9 |
18,5 |
|
2 |
78,2 |
73,4 |
8,3 |
10,6 |
12,4 |
9,8 |
13,2 |
16,8 |
3,7 |
4,6 |
21,0 |
18,9 |
48,2 |
52,4 |
14,9 |
8,1 |
|
|
7 |
1 |
64,8 |
63,4 |
4,3 |
5,7 |
2,9 |
3,0 |
7,5 |
9,3 |
3,1 |
5,5 |
27,2 |
23,3 |
38,9 |
29,9 |
- |
1,7 |
|
2 |
67,0 |
63,4 |
7,7 |
3,9 |
4,3 |
6,4 |
11,1 |
8,3 |
5,6 |
5,5 |
21,5 |
22,7 |
34,4 |
38,3 |
2,2 |
5,0 |
|
|
8 |
1 |
64,9 |
68,4 |
4,4 |
2,8 |
1,3 |
2,8 |
5,7 |
6,8 |
1,8 |
2,2 |
13,6 |
12,0 |
27,0 |
37,0 |
0,3 |
2,2 |
|
2 |
65,4 |
65,5 |
5,4 |
6,7 |
2,7 |
2,8 |
4,8 |
5,5 |
4,0 |
4,0 |
15,6 |
16,7 |
39,7 |
34,6 |
3,6 |
3,7 |
|
|
9 |
1 |
- |
- |
- |
- |
1,1 |
0,0 |
6,6 |
7,0 |
3,8 |
3,8 |
17,7 |
17,1 |
33,4 |
33,1 |
1,8 |
2,0 |
|
2 |
- |
- |
- |
- |
0,7 |
3,7 |
4,9 |
6,3 |
3,5 |
2,8 |
21,4 |
16,8 |
26,5 |
25,2 |
2,5 |
1,6 |
|
|
10 |
1 |
57,0 |
57,7 |
3,3 |
0,4 |
2,1 |
2,4 |
5,5 |
5,8 |
3,5 |
3,0 |
21,7 |
23,9 |
35,3 |
26,5 |
0,5 |
4,3 |
|
2 |
57,1 |
52,7 |
4,2 |
2,3 |
3,6 |
3,5 |
3,9 |
5,7 |
3,2 |
3,5 |
27,0 |
32,5 |
18,0 |
18,2 |
2,0 |
2,1 |
|
|
11 |
1 |
70,6 |
75,2 |
5,3 |
6,4 |
5,7 |
1,9 |
9,5 |
7,2 |
3,5 |
2,5 |
11,0 |
18,4 |
27,0 |
33,5 |
5,1 |
3,9 |
|
2 |
77,9 |
68,2 |
3,5 |
7,1 |
1,4 |
3,0 |
8,1 |
7,4 |
2,0 |
2,8 |
16,4 |
8,1 |
35,4 |
29,3 |
2,1 |
5,0 |
|
5.8.2 Данные, представленные в таблице 13, были получены в эксперименте, в котором пары проб, отобранные от восьми образцов материала, были направлены в 11 лабораторий, и на каждой пробе были получены два результата измерений на прочность с применением сульфата магния. Пробы были массой около 100 кг (они использовались в ряде других испытаний), а испытуемые навески были массой около 350 г.
5.8.3 Таблицы 14-16 показывают расхождения между результатами измерений, различия между пробами и средние значения в элементах, рассчитанные с использованием равенств (21)-(24), только для уровня 6 эксперимента.
Подставляя в равенства (27) и (28) расхождения между результатами измерений из таблицы 14 и между пробами из таблицы 15, получаем
SSr6 = 381,66 (%)2, SSH6 = 160,5300 (%)2.
Применяя уравнения (25) и (26) к средним значениям в элементах из таблицы 16, получаем
y6 = 19,0 % (общее среднее), sy6 = 5,03 %.
Так что, используя уравнения (29)-(33), для стандартных отклонений повторяемости и воспроизводимости и стандартного отклонения, которое измеряет расхождение между пробами, получим:
Sr6 = 2,95 %, sR6 = 5,51 %, sH6 = 1,72 %.
Таблица 14 - Пример 2. Расхождения между результатами измерений для уровня 6
|
Номер пробы |
Расхождение между результатами измерений, % |
Статистика k |
|
|
1 |
1 |
2,6 |
0,624 |
|
2 |
0,1 |
0,024 |
|
|
2 |
1 |
1,1 |
0,264 |
|
2 |
2,5 |
0,600 |
|
|
3 |
1 |
7,6 |
1,825 |
|
2 |
1,4 |
0,336 |
|
|
4 |
1 |
4,0 |
0,960 |
|
2 |
8,1 |
1,945 |
|
|
5 |
1 |
1,3 |
0,312 |
|
2 |
1,8 |
0,432 |
|
|
6 |
1 |
4,4 |
1,056 |
|
2 |
2,1 |
0,504 |
|
|
7 |
1 |
3,9 |
0,936 |
|
2 |
1,2 |
0,288 |
|
|
8 |
1 |
1,6 |
0,384 |
|
2 |
1,1 |
0,264 |
|
|
9 |
1 |
0,6 |
0,144 |
|
2 |
4,6 |
1,104 |
|
|
10 |
1 |
2,2 |
0,528 |
|
2 |
5,5 |
1,320 |
|
|
11 |
1 |
7,4 |
1,777 |
|
2 |
8,1 |
1,945 |
Таблица 15 - Пример 2. Расхождения между пробами для уровня 6
|
Расхождение между пробами, % |
Статистика k |
|
|
1 |
6,75 |
1,767 |
|
2 |
4,40 |
1,152 |
|
3 |
1,00 |
0,262 |
|
4 |
2,25 |
0,589 |
|
5 |
2,05 |
0,537 |
|
6 |
2,55 |
0,668 |
|
7 |
3,15 |
0,825 |
|
8 |
3,35 |
0,877 |
|
9 |
1,70 |
0,445 |
|
10 |
6,95 |
1,819 |
|
11 |
2,55 |
0,668 |
Таблица 16 - Пример 2. Средние значения в элементах для уровня 6
|
Среднее элемента, % |
Статистика h |
|
|
1 |
26,425 |
1,475 |
|
2 |
13,750 |
-1,043 |
|
3 |
21,000 |
0,397 |
|
4 |
17,075 |
-0,382 |
|
5 |
13,425 |
-1,108 |
|
6 |
21,225 |
0,442 |
|
7 |
23,675 |
0,929 |
|
8 |
14,475 |
-0,899 |
|
9 |
18,250 |
-0,149 |
|
10 |
26,275 |
1,445 |
|
11 |
13,425 |
-1,108 |
Таблица 17 дает результаты расчетов по другим уровням.
Таблица 17 - Пример 2. Значения средних, сумм квадратов расхождений и стандартные отклонения, рассчитанные по данным всех восьми уровней в таблице 13 (исключая элементы с опущенными данными)
|
Уровень j |
Число лабораторий р´ |
Общее среднее yj, % |
Суммы квадратов расхождений, %2 |
Стандартные отклонения, % |
||||
|
SSrj |
SSRj |
syj |
srj |
sRj |
sHj |
|||
|
3 |
11 |
3,7 |
82,99 |
96,3725 |
2,62 |
1,37 |
2,56 |
1,85 |
|
5 |
11 |
4,0 |
34,70 |
11,2550 |
1,88 |
0,89 |
2,01 |
0,34 |
|
8 |
10 |
4,1 |
155,39 |
29,4225 |
3,49 |
1,97 |
3,92 |
0,00 |
|
2 |
10 |
5,0 |
83,51 |
25,2375 |
1,95 |
1,44 |
2,29 |
0,47 |
|
4 |
11 |
8,2 |
131,07 |
23,5775 |
3,10 |
1,73 |
3,47 |
0,00 |
|
6 |
11 |
19,0 |
381,66 |
160,5300 |
5,03 |
2,95 |
5,51 |
1,72 |
|
7 |
11 |
36,5 |
636,19 |
305,4775 |
7,28 |
3,80 |
7,78 |
2,58 |
|
1 |
10 |
67,4 |
529,71 |
92,9225 |
6,23 |
3,64 |
7,05 |
0,00 |
5.8.4 Рисунок 4 представляет гистограммы расхождений между результатами измерений, расхождений между пробами и средних значений в элементах для уровня 6. Графики такого типа позволяют легко определить расхождения, возникающие от различных источников (между результатами измерений, пробами и лабораториями). Рисунок 4 показывает, что в этом эксперименте на уровне 6 имеется широкая вариация в средних значениях по элементам, так что, если метод испытаний будет соответствовать спецификации, то, вероятно, будут возникать разногласия между продавцом и покупателем из-за расхождений в результатах. Расхождения между пробами, которые меньше расхождений между результатами измерений (испытаний), означают, что разница между пробами на уровне 6 не является значительной.
А, В - лаборатории № 10 и 11 соответственно.
Рисунок 4 - Пример 2. Гистограммы расхождений и средних значений из таблиц 14-16 для уровня 6
5.8.5 Значения статистик h и k, рассчитанные согласно 5.6.1, также представлены в таблицах 14-16 лишь для уровня 6. Для всех уровней эти значения изображены графически на рисунках 5-7; порядок уровней изменен так, чтобы общие средние по уровню располагались в порядке их возрастания, как показано в таблице 17. Рисунок 5 показывает, что лаборатория № 6 получила несколько высоких значений статистики k для расхождений между результатами измерений, что свидетельствует о ее худшей повторяемости по сравнению с остальными лабораториями. Рисунок 6 показывает, что три лаборатории (№ 1, 6 и 10) получили высокие значения статистики k для расхождений между пробами, что могло произойти из-за отклонений от рекомендованной процедуры подготовки испытуемых навесок из проб. Рисунок 7 показывает устойчивые положительные или отрицательные значения статистики h в большинстве лабораторий (в лабораториях № 1, 6 и 10 вновь достигнуты наибольшие значения). Это прямое доказательство того, что в большинстве лабораторий имеется систематическая погрешность, свидетельствующая, что метод измерений (испытаний) неадекватно реализуется.
Рисунок 5 - Пример 2. Проверка совместимости расхождений между результатами измерений (сгруппированных по лабораториям)
Рисунок 6 - Пример 2. Проверка совместимости расхождений между пробами (сгруппированных по лабораториям)
5.8.6 Применение анализа данных по критериям Кохрена и Граббса, как описано в 5.6.2, дает результаты, представленные в таблице 18. Установлены два выброса. В отсутствие другой информации, данные, ответственные за это, должны быть исключены, а расчеты повторены. Анализ может быть затем продолжен в направлении исследования функциональных связей таким же способом, как в эксперименте по модели с однородными уровнями, рассмотренном в ГОСТ Р ИСО 5725-2.
Рисунок 7 - Пример 2. Проверка совместимости средних значений в элементах (сгруппированных по лабораториям)
Таблица 18 - Пример 2. Значения статистик Кохрена и Граббса
|
Уровень j |
Число лабораторий р´ |
Статистика Кохрена для расхождений между результатами измерений |
Статистика Кохрена для расхождений между пробами |
||||
|
3 |
11 |
0,203 |
0,664* (1) |
||||
|
5 |
11 |
0,461** (6) |
0,374 |
||||
|
8 |
10 |
0,298 |
0,465 |
||||
|
2 |
10 |
0,232 |
0,238 |
||||
|
4 |
11 |
0,169 |
0,550 |
||||
|
6 |
11 |
0,172 |
0,301 |
||||
|
7 |
11 |
0,157 |
0,536 |
||||
|
1 |
10 |
0,237 |
0,680* (6) |
||||
|
Статистика Граббса для средних значений в элементах |
|||||||
|
Уровень j |
Число лабораторий р´ |
Одно наименьшее |
Два наименьших |
Два наибольших |
Одно наибольшее |
||
|
3 |
11 |
0,970 |
0,791 |
0,098** (1; 6) |
2,219 |
||
|
5 |
11 |
1,396 |
0,709 |
0,302 |
2,266 |
||
|
8 |
10 |
0,849 |
- |
- |
2,643** (6) |
||
|
2 |
10 |
1,259 |
0,614 |
0,466 |
1,713 |
||
|
4 |
11 |
1,290 |
0,681 |
0,294 |
2,082 |
||
|
6 |
11 |
1,108 |
0,700 |
0,479 |
1,475 |
||
|
7 |
11 |
1,649 |
0,562 |
0,453 |
1,875 |
||
|
1 |
10 |
1,808 |
0,345 |
0,590 |
1,476 |
||
|
Примечание - Числа в скобках указывают лаборатории, которые обусловили квазивыбросы или выбросы. |
|||||||
|
Критические значения следующие: |
|||||||
|
Статистический критерий |
|
Число лабораторий |
Индекс в таблице ГОСТ Р ИСО 5725-2 |
* Квазивыброс |
**Выброс |
||
|
Тест Кохрена |
Расхождения между результатами измерений |
p´ |
p |
|
|
||
|
10 |
20 |
0,389 |
0,480 |
||||
|
11 |
22 |
0,365 |
0,450 |
||||
|
Тест Кохрена |
Расхождения между пробами |
10 |
10 |
0,602 |
0,718 |
||
|
11 |
11 |
0,570 |
0,684 |
||||
|
Тест Граббса: |
|
|
|
|
|
||
|
- для одиночного выброса |
Средние значения в элементах |
10 |
10 |
2,290 |
2,482 |
||
|
11 |
11 |
2,355 |
2,564 |
||||
|
- для пары выбросов |
Средние значения в элементах |
10 |
10 |
0,186 4 |
0,115 0 |
||
|
11 |
11 |
0,221 3 |
0,144 8 |
||||
5.9 Общие формулы для расчетов в эксперименте
Для каждого уровня j вычисляют следующие статистики.
a) Общее среднее (суммирование по i, t и k)
![]() , (39)
, (39)
где nj - число результатов измерений, включенных в сумму.
b) «Вклады» лабораторий для каждой i (суммирование по t и k)
![]() , то есть равно среднему (40)
, то есть равно среднему (40)
лаборатории минус общее среднее,
где nij - число результатов измерений, включенных в сумму.
c) «Вклады» проб для каждых i и t (суммирование по k)
![]() , то есть pавно среднему (41)
, то есть pавно среднему (41)
пробы минус среднее лаборатории,
где nijt - число результатов измерений, включенных в сумму.
d) Остатки для каждых i, t и k
![]() , то есть равно результату (42)
, то есть равно результату (42)
измерения минус среднее пробы.
e) Сумма квадратов для проб (суммирование по i)
![]() , (43)
, (43)
f) Сумма квадратов для проб (суммирование по i и t)
![]() . (44)
. (44)
g) Сумма квадратов для повторяемости (суммирование по i, t и k)
![]() . (45)
. (45)
h) Степени свободы:
![]()
![]()
![]() (46)
(46)
где p´j - число лабораторий, представивших хотя бы один результат измерений;
gj - число проб, для которых представлен по крайней мере один результат измерений;
nj - общее число результатов измерений.
i) Факторы для каждого i (суммирование по t):
![]() , (47)
, (47)
![]() . (48)
. (48)
j) Факторы (суммирование по i):
![]() , (49)
, (49)
![]() , (50)
, (50)
![]() . (51)
. (51)
k) Стандартные отклонения повторяемости srj, между пробами sHj, между лабораториями sLj и воспроизводимости sR, определяемые по формулам:
![]() , (53)
, (53)
![]() , (54)
, (54)
Примечание - Формулы (52-55) были получены с использованием статистической теории, разработанной Шеффе [7].
5.10 Пример 3. Применение общих формул
5.10.1 В качестве примера применения общих формул, необходимость которого возникает в связи с исключением некоторых результатов измерений, использованы данные примера 2 - уровень 4 (см. таблицу 19). Формулы, представленные в 5.9, дают общее среднее, указанное в таблице 19, а также суммы квадратов, степени свободы и факторы, приведенные в таблицах 20-22.
5.10.2 Применяя уравнения (52)-(55), получим:
![]() = 36,895 0/16 %2,
= 36,895 0/16 %2,
тогда
![]() l,52 %,
l,52 %,
и
![]()
тогда
sHj = 0,75 %,
и
![]() =
=
= [378,853 1 - (19,666 7 - 68/36) ´ 0,748 72 - 10 ´ 1,518 52]/(36 - 130/36),
тогда
sLj = 3,27 %,
и
![]()
Таблица 19 - Пример 3. Определение прочности с использованием сульфата магния для уровня 4
|
Номер пробы t |
Результат измерения, % |
||
|
k = 1 |
k = 2 |
||
|
1 |
1 |
- |
10,1 |
|
2 |
13,9 |
13,8 |
|
|
2 |
1 |
- |
- |
|
2 |
8,3 |
4,8 |
|
|
3 |
1 |
- |
7,0 |
|
2 |
- |
12,0 |
|
|
4 |
1 |
9,4 |
- |
|
2 |
- |
- |
|
|
5 |
1 |
3,7 |
6,3 |
|
2 |
3,3 |
3,7 |
|
|
6 |
1 |
16,5 |
12,3 |
|
2 |
13,2 |
16,8 |
|
|
7 |
1 |
7,5 |
9,3 |
|
2 |
11,1 |
8,3 |
|
|
8 |
1 |
5,7 |
6,8 |
|
2 |
4,8 |
5,5 |
|
|
9 |
1 |
6,6 |
7,0 |
|
2 |
4,9 |
6,3 |
|
|
10 |
1 |
5,5 |
5,8 |
|
2 |
3,9 |
5,7 |
|
|
11 |
1 |
9,5 |
7,2 |
|
2 |
8,1 |
7,4 |
|
|
Общее среднее mj = 8,1111 %. |
|||
|
Число результатов измерений nj = 36. |
|||
Таблица 20 - Пример 3. Расчет суммы квадратов для лабораторий
|
Среднее лаборатории, % |
Число результатов измерений пij |
«Вклад» лабораторий Bij, % |
Фактор Kij |
|
|
1 |
12,600 |
3 |
4,4889 |
5 |
|
2 |
6,550 |
2 |
-1,5611 |
4 |
|
3 |
9,500 |
2 |
1,3889 |
2 |
|
4 |
9,400 |
1 |
1,2889 |
1 |
|
5 |
4,250 |
4 |
-3,8611 |
8 |
|
6 |
14,700 |
4 |
6,5889 |
8 |
|
7 |
9,050 |
4 |
0,9389 |
8 |
|
8 |
5,700 |
4 |
-2,4111 |
8 |
|
9 |
6,200 |
4 |
-1,9111 |
8 |
|
10 |
5,225 |
4 |
-2,8861 |
8 |
|
11 |
8,050 |
4 |
-0,0611 |
8 |
|
Сумма квадратов для лабораторий SSLj = 378,8531 %2. |
||||
|
Степени свободы для лабораторий νLj = 11 - 1 = 10 |
||||
|
Факторы Kj = 130, K´j = 68, K j´´ = 19,6667. |
||||
Таблица 21 - Пример 3. Расчет суммы квадратов для проб
|
Номер лаборатории i |
Номер пробы t |
Среднее пробы, % |
Число результатов измерений nijt |
«Вклад» пробы Нijt, % |
|
1 |
1 |
10,10 |
1 |
-2,500 |
|
2 |
13,85 |
2 |
1,250 |
|
|
2 |
1 |
- |
0 |
- |
|
2 |
6,55 |
2 |
0,000 |
|
|
3 |
1 |
7,00 |
1 |
-2,500 |
|
2 |
12,00 |
1 |
2,500 |
|
|
4 |
1 |
9,40 |
1 |
0,000 |
|
2 |
- |
0 |
- |
|
|
5 |
1 |
5,00 |
2 |
0,750 |
|
2 |
3,50 |
2 |
-0,750 |
|
|
6 |
1 |
14,40 |
2 |
-0,300 |
|
2 |
15,00 |
2 |
0,300 |
|
|
7 |
1 |
8,40 |
2 |
-0,650 |
|
2 |
9,70 |
2 |
0,650 |
|
|
8 |
1 |
6,25 |
2 |
0,550 |
|
2 |
5,15 |
2 |
-0,550 |
|
|
9 |
1 |
6,80 |
2 |
0,600 |
|
2 |
5,60 |
2 |
-0,600 |
|
|
10 |
1 |
5,65 |
2 |
0,425 |
|
2 |
4,80 |
2 |
-0,425 |
|
|
11 |
1 |
8,35 |
2 |
0,300 |
|
2 |
7,75 |
2 |
-0,300 |
|
|
Сумма квадратов для проб SSHj = 29,9075 %2. |
||||
|
Степени свободы для проб νHj = 20 - 11 = 9. |
||||
Таблица 22 - Пример 3. Расчет суммы квадратов для повторяемости
|
Номер пробы t |
Результат измерений, % |
||
|
k = l |
k = 2 |
||
|
1 |
1 |
- |
0,00 |
|
2 |
0,05 |
-0,05 |
|
|
2 |
1 |
- |
- |
|
2 |
1,75 |
-1,75 |
|
|
3 |
1 |
- |
0,00 |
|
2 |
- |
0,00 |
|
|
4 |
1 |
0,00 |
- |
|
2 |
- |
- |
|
|
5 |
1 |
-1,30 |
1,30 |
|
2 |
-0,20 |
0,20 |
|
|
6 |
1 |
2,10 |
-2,10 |
|
2 |
-1,80 |
1,80 |
|
|
7 |
1 |
-0,90 |
0,90 |
|
2 |
1,40 |
-1,40 |
|
|
8 |
1 |
-0,55 |
0,55 |
|
2 |
-0,35 |
0,35 |
|
|
9 |
1 |
-0,20 |
0,20 |
|
2 |
-0,70 |
0,70 |
|
|
10 |
1 |
-0,15 |
0,15 |
|
2 |
-0,90 |
0,90 |
|
|
11 |
1 |
1,15 |
-1,15 |
|
2 |
0,35 |
-0,35 |
|
|
Сумма квадратов для повторяемости SSrj = 36,895 %2. |
|||
|
Степени свободы для повторяемости νrj = 36 - 20 = 16. |
|||
6 Робастные методы анализа данных
6.1 Области применения робастных методов анализа данных
6.1.1 В ГОСТ Р ИСО 5725-2 данные, полученные в эксперименте по оценке прецизионности, рекомендуют проверять двумя тестами на наличие выбросов: тестами Кохрена и Граббса; при этом любые данные, которые увеличивают тестовую статистику в том или ином из этих тестов до значений, превышающих критические на уровне 1 % значимости, должны быть отброшены (если у статистика нет обоснованного повода оставить эти данные). На практике применить эту процедуру часто нелегко. Рассмотрим результаты теста на выбросы в примере 1 в 4.8, представленные в таблице 8. Лаборатория № 5 дает только одно среднее значение в элементе (на уровне 10), достаточно экстремальное, чтобы по критерию Граббса квалифицировать его как выброс, но также дает три других квазивыброса, а данные на рисунке 3 прямо указывают, что в этой лаборатории что-то не в порядке. В этой ситуации специалист по статистике должен принять одно из решений:
a) сохранить все данные по лаборатории № 5;
b) отбросить только данные из уровня 10 по лаборатории № 5;
с) отбросить все данные лаборатории № 5.
Решение специалиста будет иметь существенное влияние на рассчитываемые значения стандартных отклонений повторяемости и воспроизводимости. В обычной практике анализа результатов экспериментов по оценке прецизионности данные, лежащие на линии, разделяющей квазивыбросы и выбросы, обнаруживаются достаточно часто, что может повлиять на результаты расчетов, что нежелательно. Робастные методы, описываемые в этом пункте, позволяют проанализировать полученные данные таким способом, при котором не требуется принимать решения, влияющие на результаты расчетов. Таким образом, если имеется основание ожидать, что результаты эксперимента по оценке прецизионности могут содержать выбросы, робастные методы могут быть предпочтительнее.
6.1.2 Основная модель, рассмотренная в разделе 5 ГОСТ Р ИСО 5725-1, содержит допущение по обоснованности установления общего значения для стандартного отклонения повторяемости для всех лабораторий, применяющих подтвержденный метод измерений. На практике часто оказывается, что некоторые лаборатории имеют худшую повторяемость, чем другие. Посмотрим, например, рисунок 5 для примера 2 в 5.8. Очевидно, что лаборатория № 6 имеет намного худшую повторяемость, чем лаборатория № 9 в этом эксперименте, так что допущение, что они достигли одинаковой повторяемости, не кажется достоверным в этом случае. Некоторые участники эксперимента по оценке прецизионности могут получать плохую повторяемость, когда метод измерений подвергается такому эксперименту впервые или когда они имеют небольшой опыт в реализации этого метода измерений. В этих ситуациях использование робастных методов будет особенно предпочтительным.
6.1.3 Примером применения робастных методов [8] является случай, когда при анализе данных эксперимента по оценке прецизионности, значения стандартных отклонений повторяемости и воспроизводимости рассчитывают таким образом, что на них не влияет наличие выбросов. Если всех участников эксперимента можно разделить на два класса: производящих данные хорошего и плохого качества, то робастные методы дадут значения стандартных отклонений повторяемости и воспроизводимости, которые действительны для класса с хорошим качеством данных, и не окажут воздействия на данные плохого качества (при условии, что класс данных плохого качества не слишком велик).
6.1.4 Использование робастных методов для анализа данных не влияет на планирование, организацию или выполнение эксперимента по оценке прецизионности. Решение об использовании робастных методов или методов выявления и удаления выбросов должно приниматься экспертом по статистике и представляться в совет экспертов. При использовании робастных методов в ходе обработки данных необходимо, как и в других случаях, проводить тесты на наличие выбросов, проверку совместимости (однородности), как это описано в ГОСТ Р ИСО 5725-2 или ГОСТ Р ИСО 5725-5, а также исследовать причины отдельных выбросов или графики по статистикам h и k. Однако сами исходные данные не должны исключаться как результаты этих измерений и проверок.
6.1.5 Знаменатели в формулах для статистик h и k являются стандартными отклонениями, которые в соответствии с методами расчета этих статистик, описанными в ГОСТ Р ИСО 5725-2, рассчитывают на основе представленных данных. Присутствие выбросов в этих данных будет изменять знаменатели, что приведет к искажениям в графиках этих статистик. Например, если на каком-то уровне эксперимента одна лаборатория выдает, что среднее значение в элементе является необычно большим выбросом, так что его величина намного больше, чем у любых других выбросов на том же уровне, то на графике статистики h это будет выглядеть в виде непомерно большого значения h для этого уровня. Однако значение статистики h для всех других лабораторий на этом же уровне будет малым, даже если несколько других лабораторий имеют выбросы. К подобному эффекту в расчетах статистики h может привести и использование общего среднего. В то же время использование робастных оценок стандартных отклонений как знаменателей в статистиках h и k и робастных оценок общих средних в расчете статистики h позволяет избежать этого искажения. Поэтому их и рекомендуется использовать для этих целей.
6.1.6 Данные эксперимента по оценке прецизионности позволяют рассчитать статистики двух типов:
a) средние значения в элементах, по которым рассчитывают стандартное отклонение, определяющее оценку межлабораторного расхождения;
b) стандартные отклонения или расхождения в пределах элементов (в том числе расхождения в эксперименте с распределенными уровнями), которые объединяют, чтобы получить оценку внутрилабораторного расхождения (вариации).
Робастные методы, описанные здесь, не подменяют эти средние значения в элементах, стандартные отклонения или расхождения (или вариации), различия, а обеспечивают альтернативные способы их сочетания для получения статистик, используемых для расчетов стандартных отклонений повторяемости и воспроизводимости.
Например, для значений одного уровня в эксперименте по модели с однородными уровнями, рассмотренном в ГОСТ Р ИСО 5725-2, первым этапом анализа является расчет среднего и стандартного отклонений результатов измерений в каждом элементе. Средние значения в элементах затем используют для расчетов стандартного отклонения, которое является оценкой межлабораторного расхождения. Когда используют робастные методы, изложенные в этом пункте, расчет выполняют с использованием Алгоритма А и средние значения в элементах не исключают из расчетов в результате применения к ним критерия Граббса. Также по этой модели эксперимента стандартные отклонения в элементах объединяют, чтобы оценить стандартное отклонение повторяемости. Если при этом использовать робастный анализ, то применяют Алгоритм S, который позволяет не исключать стандартные отклонения в элементах в результате использования критерия Кохрена. С любым подходом (описанным либо в ГОСТ Р ИСО 5725-2, либо здесь) обе эти оценки затем одинаковым образом используют для расчетов оценок стандартных отклонений повторяемости и воспроизводимости.
Более сложный пример шестифакторного ступенчато вложенного эксперимента приведен в приложении С ГОСТ Р ИСО 5725-3. Согласно этой модели первым этапом анализа является расчет средних значений по данным для каждой лаборатории (на каждом уровне), обозначаемых yi(1), ..., yi(5), и серий расхождений, обозначаемых wi(1), ..., wi(5), которые содержат информацию о вариабельности, присущей различным факторам, контролируемым в эксперименте. Для анализа данных описанными здесь робастными методами применяют Алгоритм А к средним значениям элементов, а Алгоритм S - к каждой серии расхождений по очереди. Статистики, полученные в результате этих операций, используют затем для оценок стандартных отклонений повторяемости, промежуточной прецизионности и воспроизводимости таким же образом, как и в методе анализа, описанном в ГОСТ Р ИСО 5725-3.
6.1.7 Робастные методы, включенные в эту часть ГОСТ Р ИСО 5725, были выбраны потому, что они могут быть применимы ко всем экспериментальным моделям, приведенным в частях 2-5 ГОСТ Р ИСО 5725, а также потому, что предлагаемые в них расчеты относительно просты. Необходимо заметить, однако, что при этом обеспечиваются робастные способы объединения лишь средних значений, стандартных отклонений и расхождений в элементах. Описанные робастные методы не объединяют индивидуальные результаты измерений (испытаний), то есть они начинают с арифметических средних и стандартных отклонений в элементах. Имеются, однако, методы, которые объединяют результаты измерений (испытаний) в пределах элементов робастным способом, но они могут быть более сложными при применении на практике.
6.2 Робастный анализ. Алгоритм А
6.2.1 Этот алгоритм дает робастные величины среднего и стандартного отклонений данных, к которым он применяется, а именно:
a) средним значениям в элементах для любой модели;
b) расхождениям в элементах для модели с распределенными уровнями.
6.2.2 Обозначим индексом р общее число данных, расположенных в порядке возрастания: х1, х2, …, хi, …, хp.
Обозначим робастные среднее и стандартное отклонения этих данных х* и s*.
6.2.3 Рассчитаем первоначальные значения для х* и s* в виде:
х* = медиана от хi (i = 1, 2, ..., р), (56)
s* = 1,483 ´ медиана от | хi - х*| (i =1, 2, ..., р). (57)
6.2.4 Обновим значения х* и s*, как показано ниже.
Рассчитаем
j = 1,5 s*. (58)
Для каждого значения xi (i = 1, 2, ..., р) рассчитывают:
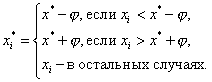 (59)
(59)
Рассчитывают новые значения х* и s* по формулам:
6.2.5 Робастные оценки х* и s* могут быть получены итеративным расчетом, то есть повторением расчетов по 6.2.4 несколько раз, до тех пор, пока изменения в оценках х* и s* от одного расчета до следующего станут минимальными. Этот метод прост для программирования на компьютере.
6.2.6 Альтернативный метод без итерации легко применим для расчетов вручную с использованием уравнений (60), (61), которые можно представить в виде:
где uL - число значений элементов xi, для которых xi < х* - j;
uU - число значений элементов xi, для которых xi > х* - j;
х´ и s´ - средние значения и стандартные отклонения (р - uL - uU) значений элементов хi, для которых| xi - х* | £ j.
Эти данные можно использовать, чтобы прямо рассчитать х* и s*, если известны uL и uU. Один из способов - проверить различные возможности, систематизировав их (то есть попытаться получить uL = 0, и uU = 0; затем uL = 0, uU = 1; затем uL = 1, uU = 0; затем uL = 1, uU = 1 и так далее) до нахождения правильного решения, в котором фактическое количество элементов, отличающихся от х* более чем на 1,5 s*, равно значениям uL и uU, использованным для расчета s* и х*. На практике аналитик может использовать гистограммы, подобные приведенным на рисунке 4, чтобы установить значения, которые вероятно отличаются от х* более чем на 1,5 s*, и таким образом найти решение, оценив малое число вариантов.
Еще одна возможность состоит в том, чтобы использовать итеративный метод для нахождения приближенного, а затем точного решения, с помощью уравнений (62) и (63). Этот подход использован в примерах, приведенных ниже.
6.3 Робастный анализ. Алгоритм S
6.3.1 Этот алгоритм применяют для внутрилабораторного стандартного отклонения (или внутрилабораторных расхождений) в любой модели эксперимента. Он дает робастное среднеквадратичное значение для стандартных отклонений или расхождений, к которым применен.
6.3.2 Обозначим индексом р общее число данных, расположенных в порядке возрастания: w1, w2, …, wi, …, wp.
(Это могут быть расхождения или стандартные отклонения).
Обозначим робастные среднеквадратичные значения w*, а число степеней свободы, связанных с каждым wi, через ν. (Когда wi - расхождение, ν = 1. Когда wi - стандартное отклонение из п результатов, ν = п - 1). В таблице 23 находим соответствующие значения ξ и η, необходимые для использования алгоритма.
6.3.3 Найдем первоначальное значение для w* в виде
w* = медиана (середина по индексам) от wi (i = 1, 2, ..., р). (64)
6.3.4 Обновляют величины w* следующим образом.
Рассчитывают
![]() . (65)
. (65)
Для каждого wi (i = 1, 2, ..., р) рассчитывают
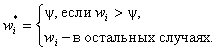 (66)
(66)
Рассчитывают новое значение w* по формуле
6.3.5 Робастная оценка w* может быть получена итеративным способом повторением расчетов по 6.3.4 несколько раз, пока изменение оценки w* от первого расчета до последующего станет минимальным. Это простой метод для программирования на компьютере.
6.3.6 Альтернативный метод без использования итерации легко применим для расчетов вручную, аналогично описанному в 6.2.6. Уравнение (67) может быть представлено в виде
где Σ΄ - суммирование тех wi, для которых wi < ψ;
иU - число wi, для которых wi > ψ.
Это можно решить подбором, положив иU = 0, иU = 1, иU = 2 и так далее до момента, при котором действительное количество значений wi, превышающих η ´ w*, станет равным иU. На практике аналитик может использовать гистограммы, подобные приведенным на рисунке 4, чтобы установить расхождения, которые вероятно превышают η ´ w*, и таким образом найти решение, оценив небольшое число вариантов.
Подход, который используют в примерах, приведенных ниже, состоит в использовании итеративного метода для приближенного решения, а затем в вычислении уравнения (68) для нахождения точного решения.
Таблица 23 - Факторы, необходимые для робастного анализа. Алгоритм S
|
Ограничительный фактор η |
Согласующий фактор ξ |
|
|
1 |
1,645 |
1,097 |
|
2 |
1,517 |
1,054 |
|
3 |
1,444 |
1,039 |
|
4 |
1,395 |
1,032 |
|
5 |
1,359 |
1,027 |
|
6 |
1,332 |
1,024 |
|
7 |
1,310 |
1,021 |
|
8 |
1,292 |
1,019 |
|
9 |
1,277 |
1,018 |
|
10 |
1,264 |
1,017 |
|
Примечание - Значения η и ξ выведены согласно приложению В. |
||
6.4 Формулы. Робастный анализ для отдельного уровня в эксперименте по модели с однородными уровнями
6.4.1 Робастная оценка стандартного отклонения повторяемости sr для какого-либо уровня этой модели может быть получена применением алгоритма S к расхождениям или стандартным отклонениям в элементах для получения робастного значения w* из уравнения (67). Если алгоритм S применяют к стандартным отклонениям в элементах, то
sr = w*. (69)
Если в элементе имеются два результата измерений и алгоритм S применяют к расхождениям в элементах, то
![]() . (70)
. (70)
6.4.2 Робастная оценка стандартного отклонения средних значений в элементах sd для некоторого уровня может быть получена применением к ним Алгоритма А, получением робастного значения s* из уравнения (61), а затем использованием равенства
sd = s*. (71)
6.4.3 Затем может быть получено межлабораторное стандартное отклонение sl на основе равенства
где n - число результатов измерений в элементе.
Если выражение под корнем отрицательное, тогда принимают
sL = 0. (73)
Стандартное отклонение воспроизводимости для определенного уровня равно
6.5 Пример 4. Робастный анализ для отдельного уровня в эксперименте по модели с однородными уровнями
6.5.1 Пример 3 в ГОСТ Р ИСО 5725-2 иллюстрирует модель с однородными уровнями, в котором данные содержат квазивыбросы и выбросы. Уровень 5 в этом примере представляет определенный интерес, поскольку лаборатория № 1 дала среднее значение в элементах, близкое к квазивыбросу по критерию Граббса, а лаборатория № 6 - по критерию Кохрена. Эти данные представлены в таблице 24.
Таблица 24 - Пример 4. Термометрическое титрование креозотного масла (% креозота)
|
Данные |
Среднее значение в элементе |
Расхождение в элементе |
||
|
1 |
24,28 |
24,00 |
24,140 |
0,28 |
|
2 |
20,40 |
19,91 |
20,155 |
0,49 |
|
3 |
19,30 |
19,70 |
19,500 |
0,40 |
|
4 |
20,30 |
20,30 |
20,300 |
0,00 |
|
5 |
20,53 |
20,88 |
20,705 |
0,35 |
|
6 |
18,56 |
16,58 |
17,570 |
1,98 |
|
7 |
19,70 |
20,50 |
20,100 |
0,80 |
|
8 |
21,10 |
20,78 |
20,940 |
0,32 |
|
9 |
20,71 |
21,66 |
21,185 |
0,95 |
6.5.2 Если сохранить данные всех лабораторий, то стандартные отклонения повторяемости и воспроизводимости могут быть оценены с использованием формул по 7.4 ГОСТ Р ИСО 5725-2, которые дают:
p = 9;
т = 20,511;
sr = 0,585;
sd = 1,727;
sL = 1,677;
sR = 1,776.
6.5.3 Однако, согласно ГОСТ Р ИСО 5725-2, аналитик использовал информацию по другим уровням в эксперименте и сомневается в идентичности проб, испытанных лабораторией № 6, чтобы оправдать исключение обеих лабораторий № 1 и № 6 из расчетов, получая:
p = 7;
т = 20,412;
sr = 0,393;
sd = 0,573;
sL = 0,501;
sR = 0,637.
Ясно, что решение об исключении данных двух лабораторий оказало существенное влияние на оценки стандартных отклонений повторяемости и воспроизводимости.
6.5.4 Первым этапом в анализе является получение робастной оценки стандартного отклонения повторяемости. Расчеты могут быть представлены согласно таблице 25, в которой расхождения в элементах рассортированы в порядке возрастания. Применяя алгоритм S, использующий итерацию, получим результаты, представленные в этой таблице. В этом примере число степеней свободы каждого расхождения в элементах составляет ν = 1, тогда ξ = 1,097 и η = 1,645. Из четырех итераций, приведенных в таблице, ясно, что робастное значение w* = 0,7, и только одно расхождение в элементе (w9* = 1,98) превышает ψ. Если бы расчеты выполнялись на компьютере, то процесс можно было бы продолжить до тех пор, пока изменение значения w* от одной итерации к следующей не станет минимальным.
Таблица 25 - Пример 4. Применение Алгоритма S к расхождениям в элементах (% креозота) (ν = l; ξ = 1,097; η = 1,645)
|
01) |
1 |
2 |
3 |
4 |
|
|
ψ |
- |
0,66 |
0,86 |
1,00 |
1,09 |
|
w1* |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
w2* |
0,28 |
0,28 |
0,28 |
0,28 |
0,28 |
|
w3* |
0,32 |
0,32 |
0,32 |
0,32 |
0,32 |
|
w4* |
0,35 |
0,35 |
0,35 |
0,35 |
0,35 |
|
w5* |
0,40 |
0,40 |
0,40 |
0,40 |
0,40 |
|
w6* |
0,49 |
0,49 |
0,49 |
0,49 |
0,49 |
|
w7* |
0,80 |
0,66 |
0,80 |
0,80 |
0,80 |
|
w8* |
0,95 |
0,66 |
0,86 |
0,95 |
0,95 |
|
w9* |
1,98 |
0,66 |
0,86 |
1,00 |
1,09 |
|
Среднеквадратичные w |
0,83 |
0,47 |
0,56 |
0,60 |
0,62 |
|
Новые w* |
0,402) |
0,52 |
0,61 |
0,66 |
0,68 |
|
1) Значения получены из таблицы 24 после перестановки в порядке возрастания. |
|||||
|
2) Медианное (срединное) расхождение [см. уравнение (64)]. |
|||||
Решение может быть также прямо получено следующим образом. Используя уравнение (68), в котором:
uU = 1,
![]()
получаем
(w*)2 = 1,0972 ´ 0,2495 + (1,097 ´ 1,645 w*)2/9,
что дает решение (если предположение, что uU = 1, корректно):
w* = 0,69 % креозота.
Можно затем подтвердить, что это значение дает ψ = 1,645 ´ 0,69 = 1,14, как и предполагалось, только w9* превышает ψ, и с последующей заменой w9* на 1,14 получаем снова w* = 0,63 ´ 1,097 = 0,69; значит, представленное решение правильно.
Следовательно, оценка стандартного отклонения повторяемости равна
sr = 0,69/![]() = 0,49 % креозота.
= 0,49 % креозота.
Это значение лежит между двумя оценками, полученными в 6.5.2 и 6.5.3.
6.5.5 Следующим этапом в анализе является получение робастной оценки стандартного отклонения средних значений в элементах. Применяя алгоритм А к средним значениям, получим результаты, представленные в таблице 26, где средние значения в элементах рассортированы в порядке возрастания. Из четырех итераций, представленных в таблице, ясно, что робастными значениями являются х* = 20,412 и s* ≈ 1,1 и что только два экстремальных средних значения в элементах (х1* = 17,570, х9* = 24,140) отличаются от х* более чем на j. Если бы расчеты выполнялись на компьютере, процесс мог бы быть продолжен, пока изменения в значениях х* и s* от одной итерации до следующей стали бы минимальными.
Таблица 26 - Пример 4. Применение Алгоритма А к средним значениям в элементах (% креозота)
|
01) |
1 |
2 |
3 |
4 |
|
|
j |
- |
1,424 |
1,478 |
1,514 |
1,539 |
|
х* - j |
- |
18,876 |
18,909 |
18,893 |
18,872 |
|
x* + j |
- |
21,724 |
21,865 |
21,921 |
21,950 |
|
x1* |
17,570 |
18,876 |
18,909 |
18,893 |
18,872 |
|
x2* |
19,500 |
19,500 |
19,500 |
19,500 |
19,500 |
|
x3* |
20,100 |
20,100 |
20,100 |
20,100 |
20,100 |
|
x4* |
20,155 |
20,155 |
20,155 |
20,155 |
20,155 |
|
x5* |
20,300 |
20,300 |
20,300 |
20,300 |
20,300 |
|
x6* |
20,705 |
20,705 |
20,705 |
20,705 |
20,705 |
|
x7* |
20,940 |
20,940 |
20,940 |
20,940 |
20,940 |
|
x8* |
21,185 |
21,185 |
21,185 |
21,185 |
21,185 |
|
x9* |
24,140 |
21,724 |
21,865 |
21,921 |
21,950 |
|
Среднее |
20,511 |
20,387 |
20,407 |
20,411 |
20,412 |
|
Стандартное отклонение |
1,727 |
0,869 |
0,890 |
0,905 |
0,916 |
|
Новые x* |
20,3002) |
20,387 |
20,407 |
20,411 |
20,412 |
|
Новые s* |
0,9492) |
0,985 |
1,009 |
1,026 |
1,039 |
|
1) Значения получены из таблицы 24 после перестановки в порядке возрастания. |
|||||
При расчете вручную аналитик должен использовать прямой метод, описанный в 6.2.6, например иL = иU = 1.
Это дает х′ = 20,412 и s′ = 0,573 % креозота.
Отсюда из уравнений (62) и (63)
(s*)2 = 6 ´ (0,573)2/[8/1,1342 - 1,52 (9 + 9 - 4)/7]
получаем s* = 1,070 % креозота и х* = х′ = 20,412 % креозота.
Можно затем подтвердить, что значение s* дает j = 1,605 (тогда как предполагалось, что только x1* и х9* отличаются от х* = 20,412 более чем на j) и что замена x1* на 18,807 и x9* на 22,017 дает новое значение х* = 20,412, а новое значение s* = 0,944 ´ 1,134 = 1,070, так что представленное решение является правильным.
Оценку межлабораторного стандартного отклонения проводят по формуле (72):
![]() % креозота,
% креозота,
а оценку стандартного отклонения воспроизводимости - по формуле (74):
![]() % креозота.
% креозота.
Снова это значение располагается между двумя оценками, полученными в 6.5.2 и 6.5.3.
6.6 Формулы. Робастный анализ для отдельного уровня в эксперименте по модели с разделенными уровнями
6.6.1 Применительно к модели с разделенными уровнями робастная оценка стандартного отклонения повторяемости sr для отдельного уровня может быть получена обработкой данных о расхождениях в элементах на определенном уровне по Алгоритму А с нахождением робастного значения s* из уравнения (61), а затем определением sr по формуле
sr = s*![]() . (75)
. (75)
6.6.2 Робастная оценка стандартного отклонения средних значений sy в элементах для уровня может быть получена применением Алгоритма А снова к средним значениям в элементах для определенного уровня, нахождением робастного значения s* из уравнения (61), а потом получением sy, с использованием равенства
sy = s*. (76)
Для оценки стандартного отклонения воспроизводимости на определенном уровне модели можно использовать формулы, приведенные в 4.5.6.
6.7 Пример 5. Робастный анализ для отдельного уровня в эксперименте по модели с разделенными уровнями
6.7.1 Данные примера 1 в 4.8 содержали несколько квазивыбросов и один выброс (см. таблицу 8). Кроме того, на рисунке 3 видна отрицательная систематическая погрешность в результатах лаборатории № 5. Если аналитик не может выявить источники этих аномалий, он попадает в трудное положение при принятии решения, какие данные следует исключить из расчетов стандартных отклонений повторяемости и воспроизводимости. Для иллюстрации результатов робастного анализа здесь использованы данные уровня 14 (см. таблицу 4).
6.7.2 Для получения робастной оценки стандартного отклонения повторяемости расхождений в элементах применяют Алгоритм А (см. таблицу 5), что приводит к результатам, показанным в таблице 27, в которой расхождения в элементах рассортированы в порядке возрастания. Из четырех итераций, представленных в таблице, видно, что робастные значения равны х* = 8,29, s* = 0,36, и что только х9* отличается от х* более чем на j.
Применяя метод, описанный в 6.2.6 при uL = 0 и uU = 1, получаем
х′ = 8,219 и s′ = 0,257 % протеина.
Тогда уравнения (62) и (63) в 6.2.6 можно записать в виде
х* = 8,219 + 1,5 ´ s*/8
и
(s*)2 = 7 ´ (0,257)2/[8/1,1342 - 1,52(0 + 9 - 0)/8],
что дает s* = 0,354 % протеина,
а, используя
уравнение (75), получим sr = 0,354/![]() = 0,250 % протеина.
= 0,250 % протеина.
Таблица 27 - Пример 5. Применение Алгоритма А к расхождениям в элементах (% протеина)
|
0 |
1 |
2 |
3 |
4 |
|
|
j |
- |
0,53 |
0,56 |
0,55 |
0,54 |
|
х* - j |
- |
7,85 |
7,74 |
7,74 |
7,75 |
|
х* + j |
- |
8,91 |
8,86 |
8,84 |
8,83 |
|
x1* |
7,81 |
7,85 |
7,81 |
7,81 |
7,81 |
|
x2* |
7,93 |
7,93 |
7,93 |
7,93 |
7,93 |
|
x3* |
8,13 |
8,13 |
8,13 |
8,13 |
8,13 |
|
x4* |
8,14 |
8,14 |
8,14 |
8,14 |
8,14 |
|
x5* |
8,38 |
8,38 |
8,38 |
8,38 |
8,38 |
|
x6* |
8,40 |
8,40 |
8,40 |
8,40 |
8,40 |
|
x7* |
8,44 |
8,44 |
8,44 |
8,44 |
8,44 |
|
x8* |
8,52 |
8,52 |
8,52 |
8,52 |
8,52 |
|
x9* |
9,31 |
8,91 |
8,86 |
8,84 |
8,83 |
|
Среднее |
8,340 |
8,300 |
8,290 |
8,288 |
8,287 |
|
Стандартное отклонение |
0,436 |
0,326 |
0,322 |
0,317 |
0,315 |
|
Новые x* |
8,3801) |
8,300 |
8,290 |
8,288 |
8,287 |
|
Новые s* |
0,3561) |
0,370 |
0,365 |
0,359 |
0,357 |
Робастное среднее значение для расхождений в элементах составляет
х* = 8,219 + 1,5 ´ 0,354/8 = 8,285 % протеина.
При этих значениях х* и s*
j = 1,5 ´ 0,354 = 0,531.
Тогда x* - j = 7,754 и х* + j = 8,816 % протеина.
Это подтверждает, что в расчетах х* и s* только х9* было вне этих пределов. Можно сделать заключение, что это тот самый случай, когда действительно найдено правильное решение.
6.7.3 Применение Алгоритма А к средним значениям в элементах (из таблицы 6) дает результаты, представленные в таблице 28, в которой средние значения в элементах расположены в порядке возрастания. Ситуация подобна представленной в таблице 26, а именно х1* и х9* отличаются более чем на j от х* и х* устремляется к среднему значению от х2* до х8*, равному 85,486. Применяя вновь метод из 6.2.6, но со значениями ul = иU = 1, получим, что среднее значение и стандартное отклонение от х2* до х8* составят:
х΄ = 85,486 и s΄ = 0,209.
Значит, на основе уравнения (63) может быть получено s* из равенства
(s*)2 = 6 ´ (0,209)2/[8/1,1342 - 1,52(9 + 9 - 4)/7],
откуда s* = 0,390 % протеина.
Теперь можно вычислить х* по формуле (62) в 6.2.6, что дает x* = 85,486 % протеина. Для контроля правильности решения, рассчитывают
j = 1,5 ´ 0,390 = 0,585, х* - j = 84,901, х* + j = 86,071 % протеина.
Таблица 28 - Пример 5. Применение Алгоритма А к средним значениям в элементах (% протеина)
|
0 |
1 |
2 |
3 |
4 |
|
|
j |
- |
0,446 |
0,492 |
0,519 |
0,537 |
|
х* - j |
- |
85,104 |
85,009 |
84,971 |
84,950 |
|
х* + j |
- |
85,996 |
85,993 |
86,009 |
86,024 |
|
x1* |
84,525 |
85,104 |
85,009 |
84,971 |
84,950 |
|
x2* |
85,140 |
85,140 |
85,140 |
85,140 |
85,140 |
|
x3* |
85,345 |
85,345 |
85,345 |
85,345 |
85,345 |
|
x4* |
85,385 |
85,385 |
85,385 |
85,385 |
85,385 |
|
x5* |
85,550 |
85,550 |
85,550 |
85,550 |
85,550 |
|
x6* |
85,575 |
85,575 |
85,575 |
85,575 |
85,575 |
|
x7* |
85,660 |
85,660 |
85,660 |
85,660 |
85,660 |
|
x8* |
85,750 |
85,750 |
85,750 |
85,750 |
85,750 |
|
x9* |
86,170 |
85,996 |
85,993 |
86,009 |
86,024 |
|
Среднее |
85,456 |
85,501 |
85,490 |
85,487 |
85,487 |
|
Стандартное отклонение |
0,453 |
0,289 |
0,305 |
0,316 |
0,324 |
|
Новые х* |
85,5501) |
85,501 |
85,490 |
85,487 |
85,487 |
|
Новые s* |
0,2971) |
0,328 |
0,346 |
0,358 |
0,367 |
Очевидно, что, как и предполагалось, только х1* и х9* выпадают из этих пределов.
Для получения стандартного отклонения воспроизводимости используют уравнение (76) в 6.6.2, которое дает sy = 0,390 % протеина, а затем уравнение (13) в 4.5.6, чтобы получить sR = 0,410 % протеина.
Из этого примера следует, что робастный метод дает несколько меньшие оценки sr и sr, чем значения, получаемые при использовании всех представленных данных (см. в таблицу 7).
6.8 Формулы. Робастный анализ для отдельного уровня эксперимента на гетерогенном материале
a) Применяют Алгоритм S к расхождениям между результатами испытаний, чтобы получить робастное значениеw * из уравнения (67), и определяют
SSr = 2 p׳ (w*)2. (77)
b) Применяют Алгоритм S к расхождениям между пробами, чтобы получить другое робастное значение w* из уравнения (67), и определяют
SSH = p׳ (w*)2. (78)
c) Применяют Алгоритм А к средним значениям в элементах, чтобы получить робастное значение s* из уравнения (61), и находят
sy = s*. (79)
Эти расчеты могут быть удобно представлены в табличной форме, с размещением в первой графе значений расхождений или средних значений в порядке возрастания, как это показано на примерах, описанных ниже.
6.8.2 Затем для расчетов оценок стандартных отклонений повторяемости и воспроизводимости и стандартного отклонения sh, которое оценивает различие между пробами, могут быть использованы формулы подраздела 5.5.
6.9 Пример 6. Робастный анализ для отдельного уровня эксперимента на гетерогенном материале
6.9.1 Данные для уровня 6 в примере 2 (см. 5.8) не содержат выбросов или квазивыбросов, и они были использованы для иллюстрации результатов, которые получают робастным анализом в таком случае.
6.9.2 Применение Алгоритма S к расхождениям между результатами измерений (из таблицы 14) иллюстрируется данными, представленными в таблице 29. Здесь число степеней свободы ν = 1, так что η = 1,645, ξ = 1,097 и число индексированных значений р = 2р΄ = 22. Из четырех итераций, представленных в таблице, видно, что робастным значением является w* ≈ 4,5 и что значения от w19* до w22* превышают ψ. Определив Σ΄ и uU как в 6.3.6, имеем
uU = 4.
Σ΄(wi*)2/р = 137,92/22 = 6,2691,
так что уравнение (68) принимает вид
(w*)2 = 1,0972 ´ 6,2691 + 4 (1,097 ´ 1,645 w*)2/22.
Отсюда получаем w* = 4,30 %.
Таблица 29 - Пример 6. Применение Алгоритма S к расхождениям между результатами измерений (ν = 1; ξ= 1,097; η = 1,645)
|
0 |
1 |
2 |
3 |
4 |
|
|
ψ |
- |
3,9 |
5,1 |
5,9 |
6,4 |
|
w1* |
0,1 |
0,1 |
0,1 |
0,1 |
0,1 |
|
w2* |
0,6 |
0,6 |
0,6 |
0,6 |
0,6 |
|
w3* |
1,1 |
1,1 |
1,1 |
1,1 |
1,1 |
|
w4* |
1,1 |
1,1 |
1,1 |
1,1 |
1,1 |
|
w5* |
1,2 |
1,2 |
1,2 |
1,2 |
1,2 |
|
w6* |
1,3 |
1,3 |
1,3 |
1,3 |
1,3 |
|
w7* |
1,4 |
1,4 |
1,4 |
1,4 |
1,4 |
|
w8* |
1,6 |
1,6 |
1,6 |
1,6 |
1,6 |
|
w9* |
1,8 |
1,8 |
1,8 |
1,8 |
1,8 |
|
w10* |
2,1 |
2,1 |
2,1 |
2,1 |
2,1 |
|
w11* |
2,2 |
2,2 |
2,2 |
2,2 |
2,2 |
|
w12* |
2,5 |
2,5 |
2,5 |
2,5 |
2,5 |
|
w13* |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
|
w14* |
3,9 |
3,9 |
3,9 |
3,9 |
3,9 |
|
w15* |
4,0 |
3,9 |
4,0 |
4,0 |
4,0 |
|
w16* |
4,4 |
3,9 |
4,4 |
4,4 |
4,4 |
|
w17* |
4,6 |
3,9 |
4,6 |
4,6 |
4,6 |
|
w18* |
5,5 |
3,9 |
5,1 |
5,5 |
5,5 |
|
w19* |
7,4 |
3,9 |
5,1 |
5,9 |
6,4 |
|
w20* |
7,6 |
3,9 |
5,1 |
5,9 |
6,4 |
|
w21* |
8,1 |
3,9 |
5,1 |
5,9 |
6,4 |
|
w22* |
8,1 |
3,9 |
5,1 |
5,9 |
6,4 |
|
Новые w |
4,17 |
2,80 |
3,29 |
3,55 |
3,70 |
|
Новые w* |
2,351) |
3,07 |
3,61 |
3,89 |
4,06 |
|
1) Получено по формуле (64). |
|||||
Подтверждением правильности решения по определению w* является то, что если w* = 4,3 %, то ψ = 7,1 и четыре значения от w19* до w22* превышают ψ. Используя уравнение (77), получим
SSr = 22 ´ 4,302 = 406,78 %2.
6.9.3 Применяя второй раз Алгоритм S к расхождениям между пробами (из таблицы 15), получаем результаты, приведенные в таблице 30. Из четырех итераций, представленных в этой таблице, видно, что робастным значением является w* = 40 и что w10* и w11* превышают ψ.
Определив Σ΄ и uU, как в 6.3.6, в этом случае имеем:
uU = 2,
Σ΄(wi*)2/p΄ = 66,665/11 = 6,0605,
так что уравнение (68) принимает вид
(w*)2 = 1,0972 ´ 6,0605 + 2 (1,097 ´ 1,645 w*)2/11.
Отсюда получаем w* = 4,23 %.
Таблица 30 - Пример 6. Применение Алгоритма S к расхождениям между пробами (ν = 1; ξ= 1,097; η = 1,645)
|
0 |
1 |
2 |
3 |
4 |
|
|
ψ |
- |
4,19 |
5,43 |
6,10 |
6,45 |
|
w1* |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
|
w2* |
1,70 |
1,70 |
1,70 |
1,70 |
1,70 |
|
w3* |
2,05 |
2,05 |
2,05 |
2,05 |
2,05 |
|
w4* |
2,25 |
2,25 |
2,25 |
2,25 |
2,25 |
|
w5* |
2,55 |
2,55 |
2,55 |
2,55 |
2,55 |
|
w6* |
2,55 |
2,55 |
2,55 |
2,55 |
2,55 |
|
w7* |
3,15 |
3,15 |
3,15 |
3,15 |
3,15 |
|
w8* |
3,35 |
3,35 |
3,35 |
3,35 |
3,35 |
|
w9* |
4,40 |
4,19 |
4,40 |
4,40 |
4,40 |
|
w10* |
6,75 |
4,19 |
5,43 |
6,10 |
6,45 |
|
w11* |
6,95 |
4,19 |
5,43 |
6,10 |
6,45 |
|
Новые w |
3,82 |
3,01 |
3,38 |
3,58 |
3,69 |
|
Новые w* |
2,551) |
3,30 |
3,71 |
3,92 |
4,05 |
|
1) Получено по формуле (64). |
|||||
К сожалению, этому соответствует значение ψ = 1,645 ´ 4,23 = 6,96, и это - недействительное решение, так как w10* и w11* не превышают 6,96. Значит, для нахождения действительного решения нужно испытать uU = 1 и uU = 0.
Приняв uU = 1, получаем
Σ΄(wi*)2/р΄ = 112,2275/11 = 10,2025.
Тогда уравнение (68) примет вид
(w*)2 = l,0972 ´ 10,202 5 + (1,097 ´ l,645 w*)2/11.
Отсюда получаем w* = 4,18 %.
Теперь ψ = 1,645 ´ 4,18 = 6,88, и можно убедиться в действительности решения, так как только w11* превышает это значение.
Используя уравнение (78) в 6.8.1, получим
SSH = 11 ´ 4,182 = 192,20 %2.
6.9.4 Применяя Алгоритм А к средним значениям в элементах (из таблицы 16), получим результаты, представленные в таблице 31. Расчеты сошлись после двух итераций и дали s* = 5,70 (при этом ни одно хi*, не отличается от х* более чем на j).
Таблица 31 - Пример 6. Применение Алгоритма А к средним значениям в элементах (%)
|
0 |
1 |
2 |
3 |
4 |
|
|
j |
- |
10,005 |
8,550 |
|
|
|
х* - j |
- |
8,245 |
10,450 |
|
|
|
х* + j |
- |
28,255 |
27,550 |
|
|
|
x1* |
13,425 |
13,425 |
13,425 |
|
|
|
x2* |
13,425 |
13,425 |
13,425 |
|
|
|
x3* |
13,750 |
13,750 |
13,750 |
|
|
|
x4* |
14,475 |
14,475 |
14,475 |
|
|
|
x5* |
17,075 |
17,075 |
17,075 |
|
|
|
x6* |
18,250 |
18,250 |
18,250 |
|
|
|
x7* |
21,000 |
21,000 |
21,000 |
|
|
|
x8* |
21,225 |
21,225 |
21,225 |
|
|
|
x9* |
23,675 |
23,675 |
23,675 |
|
|
|
x10* |
26,275 |
26,275 |
26,275 |
|
|
|
x11* |
26,425 |
26,425 |
26,425 |
|
|
|
Среднее |
19,00 |
19,00 |
19,00 |
|
|
|
Стандартное отклонение |
5,03 |
5,03 |
5,03 |
|
|
|
Новые х* |
18,251) |
19,00 |
19,00 |
|
|
|
Новые s* |
6,671) |
5,70 |
5,70 |
|
|
Используя уравнение (79), получим
sy = 5,70 %.
6.9.5 С использованием результатов, полученных в 6.9.2-6.9.4, уравнения (29)-(33) в 5.5.5 теперь дают:
s2r = 406,78/44 %2,
s2R = 5,702 + (406,78 - 192,20)/44 %2,
s2H = 192,20/22 - 406,78/88 %2.
Тогда
s2r = 3,04%,
s2R = 6,11 %,
s2H = 2,03 %.
Следовательно, в этом примере робастный метод дает оценки sr, sr и sh, которые незначительно больше значений, полученных при использовании всех представленных данных (содержащихся в 5.8.3 и таблице 17).
ПРИЛОЖЕНИЕ А
(обязательное)
Условные обозначения и сокращения, используемые в ГОСТ Р ИСО 5725
а Отсекаемый на оси ординат отрезок в соотношении s = а + bт
А Показатель, используемый для расчета неопределенности оценки
b Угловой коэффициент прямой в соотношении s = а + bт
В Лабораторная составляющая систематической погрешности измерений при реализации конкретного метода - разность между систематической погрешностью лаборатории при реализации конкретного метода измерений (конкретной МВИ) и систематической погрешностью метода измерений
B0 Составляющая величины В, представляющая все факторы, которые не изменяются в условиях промежуточной прецизионности
B(1), B(2) и т.д. Составляющие величины В, представляющие факторы, которые изменяются в условиях промежуточной прецизионности
с Отсекаемый на оси ординат отрезок в соотношении lg s = с + d lg т
С, С´, С˝ Тестовые статистики
Сcrit, С´crit, С˝crit Критические значения для статистик
CDp Критическая разность для вероятности Р
CRp Критический диапазон для вероятности Р
d Угловой коэффициент прямой в соотношении lg s = с + d lg m
е Составляющая результата измерений, представляющая случайную погрешность каждого результата измерений
f Коэффициент критического диапазона
Fp (ν1, ν2) р-квантиль F-распределения с ν1 и ν2 степенями свободы
G Статистика Граббса
h Статистика Манделя для межлабораторной совместимости
k Статистика Манделя для внутрилабораторной совместимости
LCL Нижний предел контроля (действия либо предупреждения)
т Общее среднее значение измеряемой характеристики; уровень
М Количество факторов, рассматриваемых в условиях промежуточной прецизионности
N Количество повторений (итераций)
n Количество результатов измерений, полученных в одной лаборатории на одном уровне (т.е. в пределах ячейки - базового элемента)
р Количество лабораторий, участвующих в межлабораторном эксперименте
Р Вероятность
q Количество уровней измеряемой характеристики в межлабораторном эксперименте
r Предел повторяемости (сходимости)
R Предел воспроизводимости
RM Стандартный образец
s Оценка стандартного отклонения
ŝ Прогнозируемое стандартное отклонение
Т Итог или сумма какого-либо выражения
t Количество объектов испытаний или групп объектов
UCL Верхний предел контроля (действия либо предупреждения)
W Весовой коэффициент, используемый при расчете взвешенной регрессии
w Диапазон изменения выборки результатов измерений
х Заданная величина, используемая для критерия Граббса
у Результат измерений (испытаний)
![]() Среднее
арифметическое значение результатов измерений (испытаний)
Среднее
арифметическое значение результатов измерений (испытаний)
![]() Общее среднее значение
результатов измерений (испытаний)
Общее среднее значение
результатов измерений (испытаний)
a Уровень значимости
b Вероятность ошибки второго рода
g Отношение стандартного отклонения воспроизводимости к стандартному отклонению повторяемости (сходимости) (sR/sr)
D Систематическая погрешность лаборатории при реализации конкретного стандартного метода измерений (конкретной МВИ)
![]() Оценка
D
Оценка
D
δ Систематическая погрешность метода измерений
![]() Оценка
δ
Оценка
δ
λ Поддающаяся обнаружению разность между систематическими погрешностями двух лабораторий при реализации одного и того же метода измерений или систематическими погрешностями двух методов измерений (МВИ) одного и того же назначения на идентичных образцах
μ Истинное или принятое опорное значение измеряемой величины (характеристики)
ν Число степеней свободы
ρ Поддающееся обнаружению соотношение между стандартными отклонениями повторяемости (сходимости) для методов В и А
s Истинное (действительное) значение стандартного отклонения
t Составляющая результата измерений, представляющая изменение, обусловленное временем, прошедшим с момента последней калибровки
j Поддающееся обнаружению соотношение между квадратными корнями из межлабораторных средних квадратов для методов В и А
χp2(ν) p-квантиль χ2-распределения с ν степенями свободы
Символы, используемые в качестве подстрочных индексов
С Различие, определяемое калибровкой
Е Различие, определяемое оборудованием
i Идентификатор для конкретной лаборатории
I( ) Идентификатор для промежуточных мер прецизионности; в скобках - идентификация типа промежуточной ситуации
j Идентификатор для уровня (ГОСТ Р ИСО 5725-2)
Идентификатор для группы испытаний или для фактора (ГОСТ Р ИСО 5725-3)
k Идентификатор для конкретного результата испытаний в лаборатории i на уровне j
L Межлабораторный
m Идентификатор для поддающейся обнаружению систематической погрешности
М Различие, обусловленное неидентичностью проб (образцов)
О Различие, определяемое сменой оператора
Р Вероятность
r Повторяемость
R Воспроизводимость
Т Различие, обусловленное периодом (временем), в течение которого проводят измерения или оценочный эксперимент
W Внутрилабораторный
1, 2, 3 … Для результатов измерений, нумеруемых в порядке их получения
(1), (2), (3) … Для результатов измерений (испытаний), нумеруемых в порядке возрастания измеряемой величины
Дополнительные условные обозначения и сокращения, использованные в ГОСТ Р ИСО 5725-5
D Расхождение в пределах базового элемента в эксперименте с разделенными уровнями
g Число проб (образцов), испытанных в лаборатории на одном уровне
Н Составляющая погрешности результата измерения, представляющая случайную погрешность, вызванную неоднородностью (различиями) проб (пробы)
К Функция числа результатов измерений в элементах
р΄ Число лабораторий, участвующих в межлабораторном эксперименте
SS Сумма квадратов
uL Число значений ниже нижнего предела в робастном анализе
uU Число значений выше верхнего предела в робастном анализе
z Остаток
Ф Отношение стандартных отклонений
j Предел, используемый в робастном анализе (Алгоритм А)
η Ограничивающий фактор, используемый в робастном анализе (Алгоритм S)
ψ Предел, используемый в робастном анализе (Алгоритм S)
ξ Согласующий фактор, используемый в робастном анализе (Алгоритм S)
Дополнительные условные обозначения, используемые в качестве подстрочных индексов в ГОСТ Р ИСО 5725-5
а, b Идентификаторы для проб в эксперименте по модели с разделенными уровнями
t Идентификатор для пробы в лаборатории i на уровне j
Н Между пробами
Дополнительное условное обозначение, используемое в качестве надстрочного индекса в ГОСТ Р ИСО 5725-5
* Робастная оценка
ПРИЛОЖЕНИЕ В
(справочное)
Вывод факторов, используемых в Алгоритмах А и S
B.1 Введение
Использование
робастных методов анализа данных экспериментов по оценке прецизионности
предложено Комитетом аналитических методов Королевского Химического Общества
Соединенного Королевства [8].
Алгоритм А в настоящем стандарте взят из публикации так же, как и коэффициент
1,134, использованный для расчета s* в Алгоритме А
(это значение ![]() для случая с =
1,5).
для случая с =
1,5).
Алгоритм S схож с процедурой, приведенной в [8] для специального случая, в котором каждая лаборатория представляет п = 2 измерений для каждого уровня. Это делает удобным применение метода робастного анализа в экспериментах по оценке прецизионности с более чем двумя факторами (такими, как эксперимент для гетерогенного материала в разделе 5 настоящего стандарта и модели в ГОСТ Р ИСО 5725-3). Вывод факторов, используемых в алгоритме S, приведен ниже.
B.2 Условные обозначения, применяемые в настоящем приложении
s - истинное (действительное) стандартное отклонение,
s - стандартное отклонение, дающее оценку ст,
ν - число степеней свободы для s,
ω - ν + 2,
ξ - согласующий фактор для алгоритма S,
η - ограничительный фактор для алгоритма S,
χν2 - распределение χ2 с ν степенями свободы
![]()
B.3 Вывод ограничительного фактора η и согласующего фактора ξ
Согласующий фактор ξ определен как значение, необходимое для регулирования s* таким образом, чтобы (s*)2 давала несмещенную оценку s2, не отягощенную систематической погрешностью, то есть
E {(ξ ´ s*)2} = s2. (В.1)
Это требование может быть записано в виде
E = {ν (s*/s)2} = ν/ξ2, (B.2)
где случайная величина в фигурных скобках, тесно связанная с ν (s*/s)2, имеет распределение χν2.
Плотность вероятности распределения χν2 равна
f(х) = е-x/2 x(ν/2-1) 2-ν/2/Г (ν/2), (В.3)
так что
потому что предел s < η s эквивалентен ν (s*/s)2 £ ν η2.
Второй член в правой части (В.4) равен
ν η2 ´ P (χν2 > ν η2) = ν η2 ´ P (x > η s). (B.5)
Для Алгоритма S ограничительный фактор η выбран так, что параметр η s является верхней 10 %-ной точкой распределения s, то есть
P (s > η s) = 0,1. (B.6)
Биометрические таблицы для распределения χ2 дают значения η, представленные в таблице 23 настоящего стандарта. Равенства (В.5) и (В.6) означают, что второй член в правой части уравнения (В.4) равен 0,1 ν η2. Заметим, что η зависит от числа степеней свободы для s.
Первый член в правой части уравнения (В.4) можно представить в виде
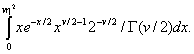
При ω = ν + 2 хорошо известное свойство гамма-функции имеет вид
Г (ω/2) = Г (ν/2 + 1) = (ν/2) ´ Г (ν/2).
Тогда этот первый член можно переписать в виде
Следовательно, для данного числа степеней свободы ν фактор η может быть рассчитан, как это описано выше, и тогда z может быть оценен снова с использованием значений χ2, приведенных в биометрических таблицах. Таким образом, оба члена правой части уравнения (В.4) могут быть оценены
Подстановка равенств (В.2), (В.5), (В.6) и (В.7) в (В.4) дает
ν/ξ2 = ν ´ z+0,1 ν η2
или
![]() (B.8)
(B.8)
Это равенство может быть использовано для получения значений согласующего фактора ξ, представленных в таблице 23 настоящего стандарта.
ПРИЛОЖЕНИЕ С
(справочное)
Вывод равенств, используемых для робастного анализа
Равенства (62) и (63), используемые для расчета робастных величин среднего значения и стандартного отклонения методом, описанным в 6.2.6, могут быть получены из соотношений (60) и (61) Алгоритма А следующим образом.
С обозначениями, принятыми в 6.2.4 и 6.2.6:
![]() (C.2)
(C.2)
и
где ![]() - суммирование (р
- uL - uU) значений по пунктам хi, для которых | хi - хi*|£ j .
- суммирование (р
- uL - uU) значений по пунктам хi, для которых | хi - хi*|£ j .
Значит, уравнение (С.1) может быть записано в виде
![]()
Тогда
![]()
или
![]() (C.4)
(C.4)
что является равенством (62).
Для получения уравнения (63) из уравнения (61) заметим, что сумма в уравнении (61) может быть представлена следующим образом:
![]() (C.5)
(C.5)
Подставляя х* в сумму в правой части выражения для х*, после некоторых алгебраических преобразований получим
![]() (C.6)
(C.6)
Используя определение s΄ в уравнении (С.3), можно записать
Подставив уравнение (С.7) в уравнение (61), получим уравнение (63).
ПРИЛОЖЕНИЕ D
(справочное)
Библиография
[1] ISO 3534-1:1993 Statistics-Vocabulary and symbols - Part 1: Statistical methods. Terms and definitions
[2] Youden, W.J. The Youden plot. Industrial Quality Control
[4] BS 3144:1968, Methods og fampling and physical testing of leather. British Standards Institution
[5] BS 812-103:1985, Testing aggregates - Part 103: Methods for determination of particle size distribution. British Standards Institution
[7] Scheffe, H. The analysis of variance. Wiley, New York, 1959
[8] Analytical Methods Committee. Robust statistics - How not to reject outliers. Part 1: Basic concepts. Part 2: Inter-laboratory trials. The Analyst
[9] SWEENEY, An inter-laboratory study of the determination of protein by combustion in feeds. Journal of the Association of Official Analytical Chemists
Ключевые слова: измерение, испытания, метод измерений, стандартизация метода измерений, результаты измерений, результаты испытаний, точность, правильность, прецизионность, систематическая погрешность, повторяемость, воспроизводимость, статистический анализ, робастные методы анализа данных, статистическая модель эксперимента с гетерогенным материалом